Pythagoraan lause

Kuva 1

Kuva 2

Pythagoraan lauseen avulla voidaan laskea suorakulmaisen kolmion yhden sivun pituus, jos kaksi muuta sivua tunnetaan.

Pythagoraan lause kertoo suorakulmaisen kolmion sivujen pituuksista seuraavan merkittävän seikan:

Kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö.

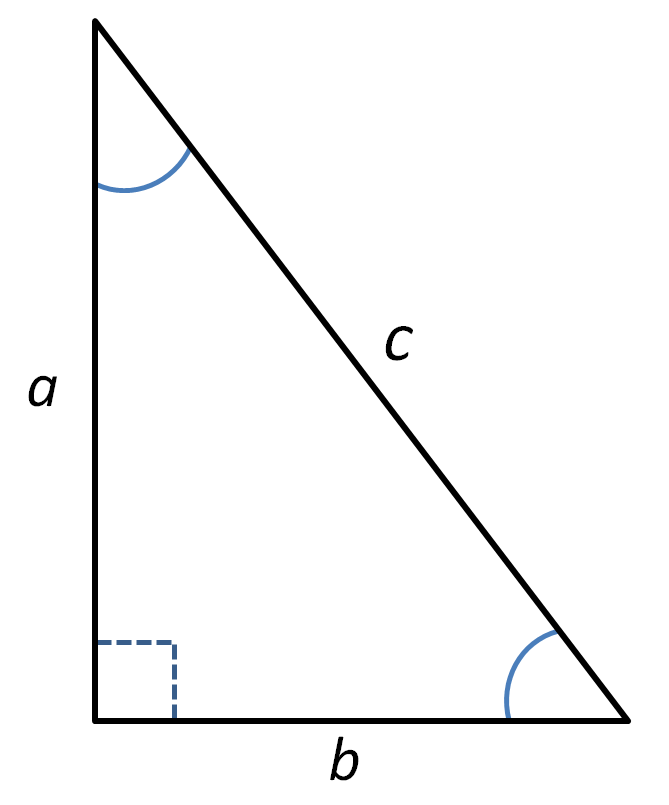
Kaavana sama asia ilmaistaan seuraavasti (kirjaimet \(a\), \(b\) ja \(c\) ovat sivujen pituuksia kuvassa 1):

\begin{equation*}a^2+b^2=c^2\end{equation*}

Esimerkki

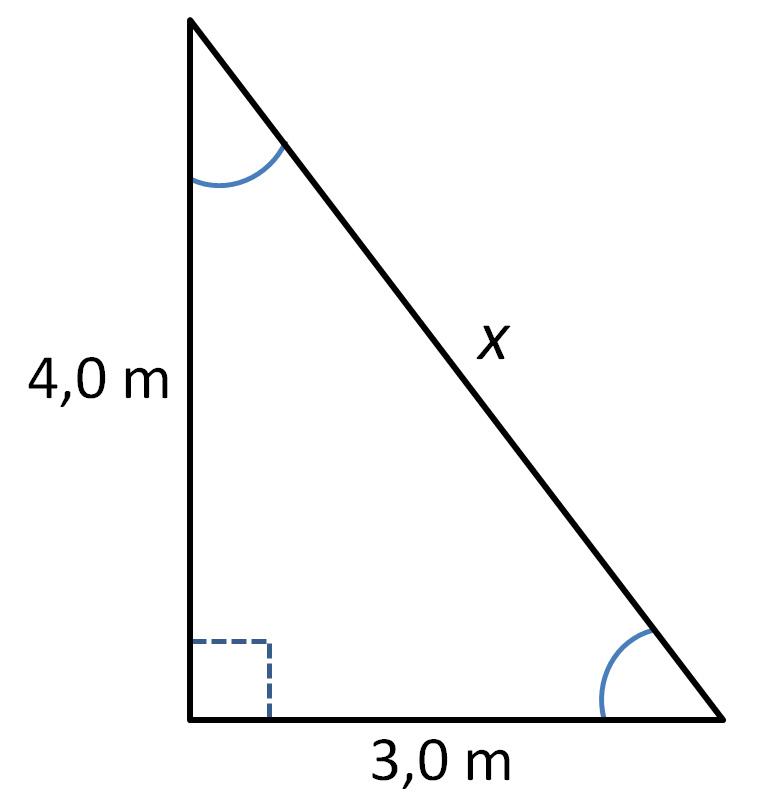
Kuvan 2 hypotenuusan pituus saadaan Pythagoraan lauseen avulla selville. Laskusta voidaan jättää yksiköt pois, kun pidetään huoli siitä, että kyse on koko ajan metreistä.

\begin{align*} 4,0^2+3,0^2&=x^2 \quad \Vert \:\text{puolten vaihto}\\ x^2&=4,0^2+3,0^2 \quad \Vert \sqrt{}\\ \left |x\right |&=\sqrt{4,0^2+3,0^2}=\sqrt{16+9,0}=\sqrt{25}=5,0 \\ x&=\pm 5,0 \end{align*}

Vastaus: Hypotenuusan pituus on 5,0 metriä.

Huomautus 1: yhtälön toinen ratkaisu on −5, mutta pituuksista puhuttaessa se voidaan jättää yleensä huomiotta.

Huomautus 2: Vastaus sattuu olemaan tarkka luku. Yleensä vastaus on likiarvo, joka pitää pyöristää järkevästi (tässä yhtä monen merkitsevän numeron tarkkuuteen kuin jolla epätarkin alkuarvo on annettu).