Suoran yhtälö

Kuva 1

Yhtälössä voi olla useampi kuin yksi muuttuja. Tarkastellaan tässä muotoa y = kx+b olevia yhtälöitä, joissa k ja b ovat vakioita.

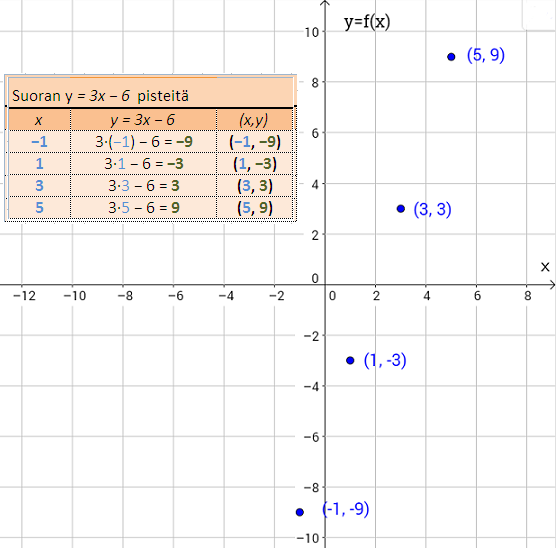Esimerkiksi yhtälössä y = 3x − 6 on kaksi muuttujaa, x ja y. Yhtälö kertoo, että y saadaan kertomalla x kolmella ja vähentämällä tuloksesta 6.

Jos x = 2, on y = 3⋅2 − 6 = 0. Tällöin lukupari (2, 0) toteuttaa yhtälön y = 3x − 6. Tällaisia lukupareja on ääretön määrä, ja koordinaatistoon sijoitettuna pisteet asettuvat suoraan linjaan (-> suoran yhtälö).

Kuvassa 1 on esitetty suoran piirtämisen vaiheet. Taulukon avulla lasketaan neljä (x,y)-lukuparia, jotka merkitään koordinaatistoon. Lopuksi piirretään suora pisteiden kautta.

Huomaa, että muuttujan x arvot saa valita vapaasti. Varmuuden vuoksi kannattaa laskea vähintään kolme (x,y)-paria, jotta mahdolliset laskuvirheet huomataan (esimerkiksi jos pisteet eivät asetu suoralle).