Kulman suuruuden laskeminen

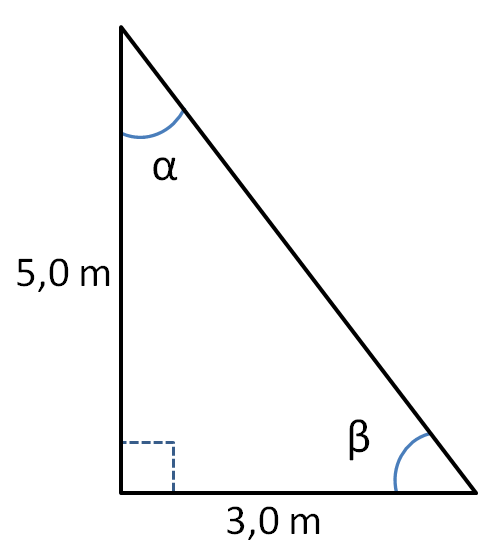
Kuva 1

Trigonometristen funktioiden avulla voidaan laskea suorakulmaisen kolmion kulmien suuruudet, jos tiedetään kolmion kahden sivun pituudet.

Laskemisen vaiheet:

1. Päätä, minkä kulman lasket ensin.
2. Selvitä kahden tunnetun sivun nimitykset valitusta kulmasta katsoen (esim. kulman vastainen kateetti ja hypotenuusa).
3. Valitse valitun kulman se trigonometrinen funktio (\(\sin\), \(\cos\) tai \(\tan\)), jonka määritelmässä esiintyvät kyseiset kaksi sivua.
4. Kirjoita yhtälö ja ratkaise se (lopussa tarvitaan usein laskinta).

Esimerkki: laske kuva 1:n kolmion terävien kulmien suuruudet.

1. Lasketaan ensin kulma α (valita voit tässä vapaasti)
2. Tunnetaan kulman α vastainen ja viereinen kateetti.
3. Kulman tangentti sopii tähän, koska siinä esiintyvät molemmat kateetit.
4. \begin{align*} \tanα &= \frac{3,0}{5,0} \\ \tanα &= 0,6 \quad \Vert \:\text{Laskimen avulla saadaan α selville: } \tan^{-1} \\ α & ≈ 31° \\ \end{align*}

Vastaus: kulman \(α\) suuruun on noin \(31°\). Kulma \(β\) saadaan tämän jälkeen helposti laskulla \(90°− 31° = 59°\).

Huomautus: kuvan kolmiossa sivujen suhteet eivät ole aivan tarkasti oikeat.