Sivun pituuden laskeminen

Kuva 1

Trigonometristen funktioiden avulla saadaan selville kolmion sivun pituus, jos tunnetaan yhden terävän kulman suuruus ja kolmion yhden sivun pituus.

Ratkaisun vaiheet:

1. Selvitä, mitkä tiedot tehtävässä on annettu ja mitä kysytään. Piirrä kuva, ellei sellaista ole.
2. Valitse sellainen trigonometrinen funktio, jonka määritelmässä olevista muuttujista kaksi tunnetaan ja kolmas on tarkoitus saada selville.
3. Muodosta yhtälö ja ratkaise se.
4. Lopuksi tarkista vastauksen mielekkyys ja muotoile vastaus niin, että se vastaa esitettyyn kysymykseen.

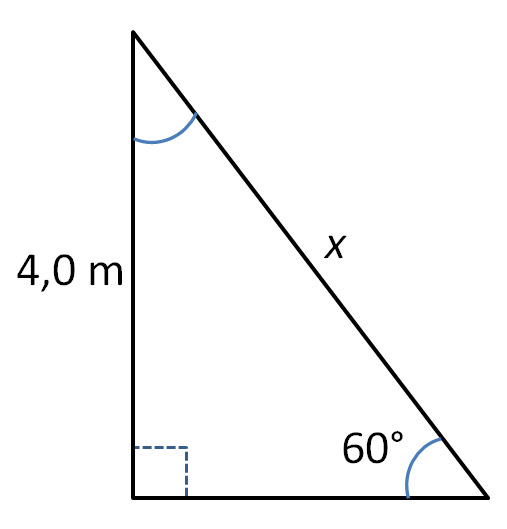
Esimerkki: Kuvassa 1 on suorakulmainen kolmio, jonka hypotenuusan pituus saadaan selville seuraavasti:

1. Kuvan kolmiossa tunnetaan yksi terävä kulma ja sen vastainen kateetti. Hypotenuusa on tuntematon, joka pitäisi selvittää.
2. Käytetään sini-funktiota, koska sen määritelmän muuttujista tunnetaan kulma ja kulman vastainen kateetti ja hypotenuusa on tarkoitus selvittää.
3. Muodostetaan yhtälö ja ratkaistaan se. Yksikkö on koko ajan metri, joten voidaan jättää se pois yhtälöstä: \begin{align*} \sin60° &= \frac{4,0 }{x} \quad \Vert \cdot x \\ x \cdot \sin60° &= 4,0 \quad \Vert :\sin60° \\ x &= \frac{4,0}{\sin60°} ≈4,62 \quad \ \\ \end{align*}
4. Vastaus: Hypotenuusan pituus on noin 4,6 metriä.

Huomautus: Vastauksen järkevyyttä tarkastellessa kannattaa verrata tulosta kolmion aiemmin tunnettuihin arvoihin ja tarkistaa ainakin, että hypotenuusa on pidempi kuin tunnetut kateetit.