Rationaalifunktiot

Kuva 1

Rationaalifunktio on funktio, joka voidaan kirjoittaa kahden polynomifunktion osamääränä. Funktio \(f(x)\) on siis rationaalifunktio, jos on olemassa polynomifunktiot \(P(x)\) ja \(Q(x)\) siten, että

\begin{equation*} f(x)=\frac{P(x)}{Q(x)} \end{equation*}

Yllä \(Q(x)\) voi olla vakiofunktio, eli jokin luku (ei nolla). Tällöin funktio \(f(x)\) on polynomifunktio.

Esimerkiksi rationaalifunktio \(R(x)\) voidaan määritellä seuraavasti:

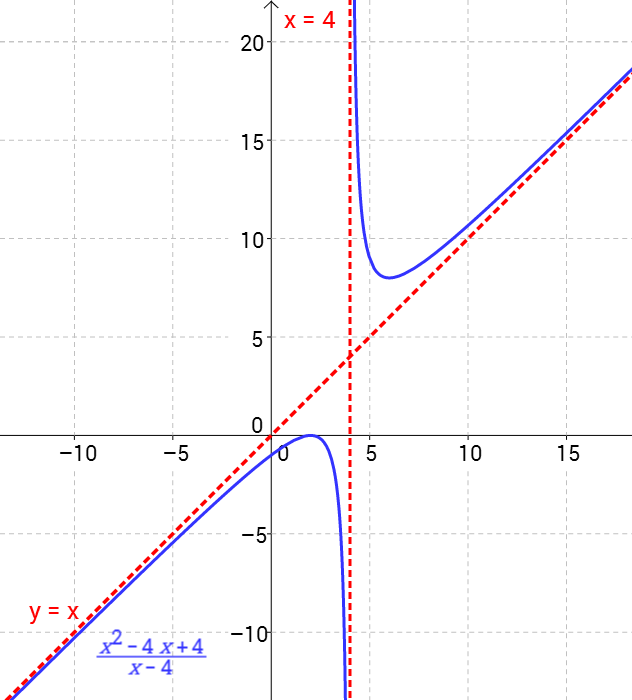
\begin{equation*} R(x) = \frac{x^2−4x+4 }{x−4} \end{equation*}

Funktion kuvaaja on kuvassa 1 (yhtenäiset siniset viivat).

Funktio \(R(x)\) voidaan esittää myös muodossa

\begin{equation*}R(x)=x+\frac{4}{x-4}\end{equation*}

joka lasketaan myös rationaalifunktioksi.

Funktiolla \(R(x)\) on kaksi suoraa asymptoottia, pystysuora ja vino (kuvassa punaiset katkoviivat).

Rationaalifunktion kuvaaja on usein hyperbeli (kaksiosainen jatkuva viiva kuvassa 1), mutta voi olla muukin käyrä.