Analyysi

Kuva 1

Kuva 2

Kuva 3

Analyysissa tutkitaan reaalilukuja ja niiden välisiä funktioita. Tyypillisiä analyysin käsitteitä ovat muun muassa raja-arvo, derivointi ja integrointi.

Alla on näistä kolmesta tyypilliset laskuesimerkit. Tarkemmat selitykset ovat kyseisissä artikkeleissa.

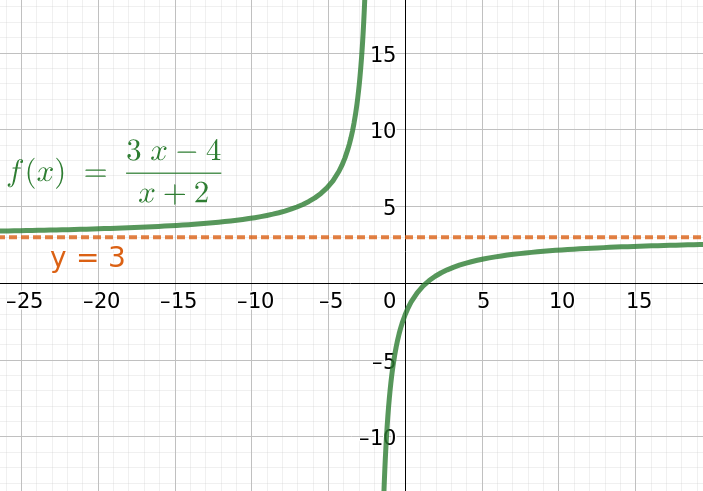
Rationaalifunktion raja-arvo (kuva 1):

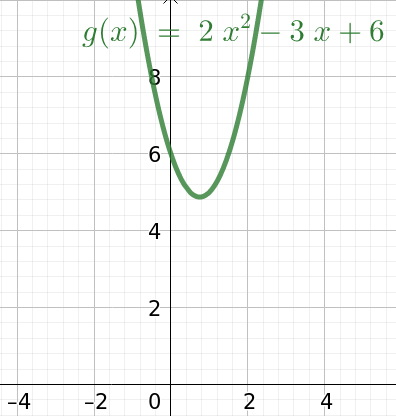
\begin{equation*} \lim_{x\to \infty}\frac{3x-4}{x+2} = \lim_{x\to \infty}\frac{3-\frac{4}{x}}{1+\frac{2}{x}} =\frac{3}{1}=3, \end{equation*} koska \begin{equation*} \lim_{x\to \infty}\frac{4}{x}=0 \:\text{ja } \lim_{x \to \infty}\frac{2}{x}=0 \end{equation*}

Funktion derivaatta ja minimiarvo (kuva 2):

Olkoon funktio \(g(x)=2x^{2}-3x+6\). Tällöin funktion derivaattafunktio on \(g'(x)=4x-3\). Lasketaan derivaatan nollakohdat:

\begin{align*} g'(x)&=0 \\ 4x-3&=0 \quad \Vert+3 \\ 4x&=3 \quad \Vert :4 \\ x&=\frac{3}{4} \end{align*}

Koska \(g\) on toisen asteen polynomifunktio ja sen kuvaaja on ylöspäin aukeava paraabeli, saadaan derivaatan nollakohdasta funktion \(g\) pienin arvo (globaali minimi):

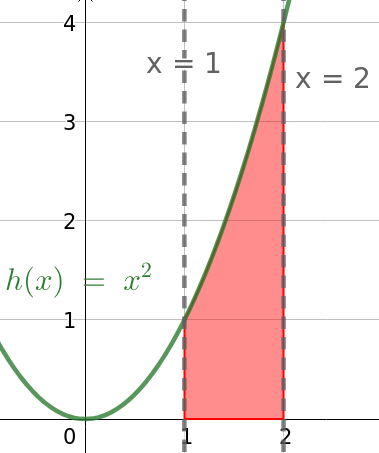
\begin{equation*} g\left (\frac{3}{4}\right ) =2 \cdot \left (\frac{3}{4}\right )^{2}-3\cdot \left (\frac{3}{4}\right )+6 \\ =2\cdot \left (\frac{9}{16}\right )-\frac{9}{4}+6 =\frac{9}{8}-\frac{9}{4}+6 \\ =\frac{9}{8}-\frac{18}{8}+6 =-\frac{9}{8}+6 =4\frac{7}{8} \end{equation*}

Integraali ja pinta-ala (kuva 3):

\begin{equation*} \int\limits_{1}^{2}x^{2} \mathrm{dx} =\left. \left (\frac{1}{3}x^{3}\right ) \right \vert_{1}^{2} =\frac{1}{3}\cdot2^{3}-\frac{1}{3}\cdot 1^{3}\\ =\frac{1}{3}\cdot 8-\frac{1}{3}\cdot 1 =\frac{8}{3}-\frac{1}{3} =\frac{7}{3} =2\frac{1}{3} \end{equation*}

Määrätyn integraalin arvo kertoo kuvassa 3 punaiseksi värjätyn alueen pinta-alan (ruutuina). Tulos on tarkka arvo.