Funktion ääriarvot

Kuva 1

Kuva 2

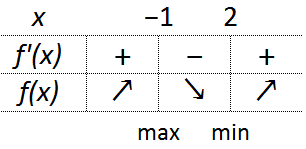Polynomifunktion kuvaaja voi muuttaa suuntaansa laskevasta nousevaksi tai nousevasta laskevaksi ainoastaan derivaatan nollakohdassa. Siinä on funktion paikallinen ääriarvo, jos nollakohdan eri puolilla on derivaatalla eri merkki \((+/−)\).

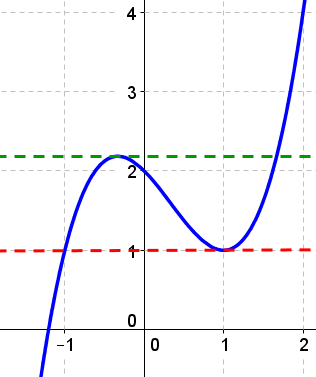
Esimerkiksi kuvan 1 funktiolla on paikallinen minimi kohdassa \(x=1\), jossa derivaatta eli tangentin (punainen katkoviiva) kulmakerroin on nolla. Kohdan \(x=1\) oikealla puolella kuvaaja on nouseva (derivaatta \(> 0\)) ja vasemmalla puolella laskeva (derivaatta \(< 0\)).

Kuvan 1 funktion derivaatalla on myös toinen nollakohta (vihreä tangentti), jossa on paikallinen maksimi.

Paikallisen ääriarvokohdan varmistamiseksi pitää useimmiten tutkia, vaihtuuko derivaatan merkki nollakohdassa. Ellei vaihdu, ei kyse ole ääriarvokohdasta, vaan niin kutsutusta terassikohdasta.

Funktion globaali ääriarvo on suurin / pienin arvo, jonka funktio voi saada määrittelyjoukossaan. Kaikilla funktioilla tällaista arvoa ei ole. Esimerkiksi funktio \(f(x)=x^3\) kasvaa / vähentyy rajatta, kun muuttujan arvo kasvaa / pienenee. Sen sijaan vaikkapa toisen asteen polynomifunktiolla on aina joko globaali minimi tai globaali maksimi (paraabelin aukeamissuunnan mukaan).

Esimerkki

Funktion \(f(x)=2x^3-3x^2-12x+10\) derivaatta on \(f'(x)=6x^2-6x-12\), jonka nollakohdat ovat \(x=2\) ja \(x=-1\) (saadaan 2. asteen yhtälön ratkaisukaavalla).

Derivaatan merkkiä nollakohtien ympärille voidaan tutkia laskemalla testiarvoja:

\(f'(-2)=6⋅(-2)^2-6⋅(-2)-12=24+12-12=24 > 0\)

\(f'(0)=6⋅0^2-6⋅0-12=-12 < 0\)

\(f'(3)=6⋅3^2-6⋅3-12=54-18-12=24 > 0\)

Tulosten perusteella voidaan piirtää kuvan 2 mukainen taulukko, josta nähdään, että funktiolla on yksi paikallinen maksimi ja yksi paikallinen minimi (nuolet viittaavat siihen, onko funktion kuvaaja nouseva vai laskeva).

Maksimin ja minimin arvot saadaan sijoittamalla derivaatan nollakohdat alkuperäiseen funktioon:

\(f(-1)=2⋅(-1)^3-3⋅(-1)^2-12⋅(-1)+10 \\=-2-3+12+10=17\) (paikallinen maksimi)

\(f(2)=2⋅2^3-3⋅2^2-12⋅2+10 \\= 16-12-24+10=-10\) (paikallinen minimi)