Derivaatan nollakohdat

Kuva 1

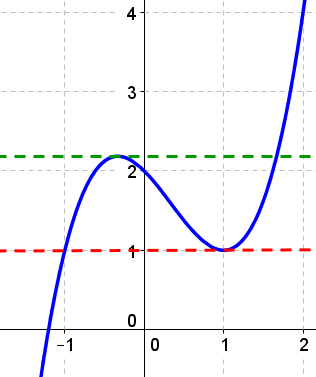Jos derivaatan arvo jossakin kohdassa on nolla, kulkee funktion kuvaaja siinä tarkalleen \(x\)-akselin suuntaisesti.

Derivaatan nollakohdat saadaan selville merkitsemällä derivaattafunktio nollaksi ja ratkaisemalla syntynyt yhtälö.

Esimerkiksi kuvan 1 funktion derivaatta on kahdessa kohtaa nolla. Näihin kohtiin on kuvassa piirretty punainen ja vihreä tangentti.

Kuvan 1 funktion \(f(x)=x^3-x^2-x+2\) derivaatta on \(f'(x)=3x^2-2x-1\) jonka nollakohdat saadaan seuraavasti:

\begin{align*} f'(x)&=0 \\ 3x^2-2x-1&=0 \quad \Vert \:\text{ratkaisukaava:}\\ x&=\frac{2\pm \sqrt{(-2)^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3} \\ &=\frac{2\pm \sqrt{4+12}}{6} \\ &=\frac{2\pm \sqrt{16}}{6} \\ &=\frac{2\pm 4}{6} \\ \end{align*}

Derivaatan nollakohdat ovat siis \(x=1\) ja \(x=-\frac{1}{3}\).

Avoimella välillä määritellyn jatkuvan funktion jokaisessa ääriarvokohdassa derivaatan arvo on nolla. Huomaa, että tämä ei välttämättä pidä paikkaansa toiseen suuntaan: derivaatan nollakohta ei ole välttämättä ääriarvokohta (ns. terassikohta). Tarkista aina esim. merkki-kulkukaavion avulla!