Yhtälö

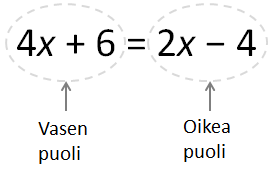Yhtälö saadaan merkitsemällä kaksi lauseketta yhtä suuriksi. Jokaisessa yhtälössä on siis yhtäsuuruusmerkki, joka jakaa yhtälön vasempaan ja oikeaan puoleen.

Esimerkkejä yhtälöistä:

a) \(4x =-2x + 2\)

b) \(y = x^2\)

c) \(\frac{5k+4}{k}=-3\)

Esimerkeissä eri kirjaimet ovat muuttujia. Muuttuja, jonka arvoa ei tunneta, on nimeltään tuntematon.

Yhtälö ratkaistaan hakemalla tuntemattomalle sellainen arvo, jolla yhtälön puolet ovat yhtä suuria. Tämä arvo on yhtälön ratkaisu eli juuri.

Esimerkki: yhtälön \(4x − 4 = x − 1\) ratkaisu on \(x = 1\), koska tällöin yhtälön vasen puoli \(4x − 4\) \(= 4 · 1 − 4 = 0\) ja yhtälön oikea puoli \(x − 1\) \(= 1 − 1 = 0\) ovat yhtä suuria (kummankin arvo on nolla).

Yhtälön ratkaisemisen säännöt:

Tavoite: muokata yhtälöä niin, että tuntematon jää yksin yhtälön toiselle puolelle, jolloin yhtälön mahdollinen ratkaisu nähdään suoraan (esim. x = 2).
Keinot: yhtälöä saa muokata, kun vain yhtälön molemmille puolille tehdään samat toimenpiteet. Tällöin uusi yhtälö on yhtäpitävä edellisen kanssa, eli muuttujan arvo on sama. Huomaa: älä kerro nollalla, koska se hävittää myös muuttujat!