Terassikohta

Joskus derivaatan nollakohta on ns. terassikohta, joka ei ole maksimi eikä minimi edes paikallisesti.

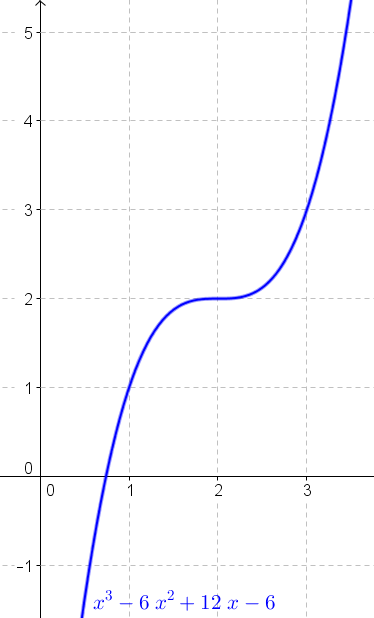
Esimerkki: tarkastellaan jatkuvaa funktiota (polynomifunktiot ovat aina jatkuvia) \(f(x)=x^3−6x^2+12x−6\), jonka derivaattafunktio on \(f′(x)=3x^2−12x+12.\) Lasketaan derivaatan nollakohdat: \begin{align*} 3x^2−12x+12&=0 \quad \Vert: 3 \\ x^2−4x+4&=0 \\ \end{align*} \begin{equation*} x=\frac{4\pm \sqrt{(-4)^2-4 \cdot 1 \cdot 4}}{2} \\ \quad=\frac{4\pm \sqrt{16-16}}{2} = \frac{4}{2}=2 \end{equation*} Derivaatta on polynomifunktiona jatkuva kaikilla reaaliluvuilla, jolloin sen merkki voi vaihtua vain derivaatan nollakohdassa \(x=2\).

Kuitenkin derivaatan merkki nollakohdin eri puolilla on positiivinen (esim. \(f′(0)=3⋅0^2−12⋅0+12 = 12 > 0\) ja \(f'(3)=3⋅3^2−12⋅3+12=27-36+12=3 > 0\)).

Toisin sanoen derivaatta vain käy nollassa, mutta jatkaa sen jälkeen kasvamista. Tässä tapauksessa kyseessä ei ole ääriarvokohta. Kuva havainnollistaa tilannetta. Derivaatan nollakohta ei ole minimi eikä maksimi missään nollakohdan ympäristössä.

Tällaista derivaatan nollakohtaa sanotaan kuvaavasti terassikohdaksi.