Soveltaminen

Kuva 1

Kuva 2

Derivaatta on hyvä työkalu tehtävissä, joissa pitää löytää funktion avulla kuvatun ilmiön maksimi- tai minimiarvoja.

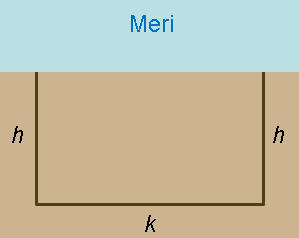
Esimerkki: Eerolla on 100 metriä aitaa. Mikä on suurimman mahdollisen suorakulmion muotoisen tontin pinta-ala, jonka Eero voi ympäröidä meren rannalta, kun meri toimii yhtenä rajana (sinne ei tarvita aitaa)?

Ratkaisu: Merkitään aidan rannan suuntaista sivua kirjaimella \(k\) ja kahta muuta (yhtä pitkää) sivua kirjaimella \(h\) (kuva 1). Koska aitaa on yhteensä 100 metriä, voidaan muuttuja \(k\) ilmaista muuttujan \(h\) avulla seuraavasti:

\begin{align*} 2h+k&=100 \quad║-2h \\ k&=-2h+100 \\ \end{align*}

Olkoon \(A(h)\) tontin pinta-alan funktio. Suorakulmion pinta-ala saadaan kertomalla kanta korkeudella, joten funktio \(A(h)\) saadaan seuraavasti:

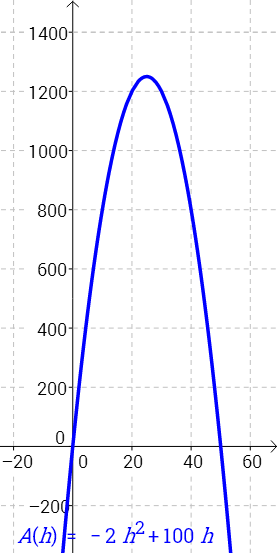
\begin{equation*}A(h)=hk=h(-2h+100) = -2h^2+100h\end{equation*}

Kysymyksessä on toisen asteen polynomifunktio (kuva 2), jonka kuvaaja on alaspäin aukeava paraabeli, jonka globaali maksimi on derivaatan nollakohdassa. Funktio on kaikkialla määritelty, mutta kysymyksen tilanteessa sivun pituus \(h\) on aina välillä \([0,50]\), jotta suorakulmio on "normaali". Toisin sanoen tässä funktion määrittelyjoukoksi sovitaan \([0,50]\).

\begin{equation*}A'(h)=-4h+100\end{equation*}

Lasketaan derivaatan nollakohta:

\begin{align*} -4h+100&=0 ║-100\\ -4h&=-100 ║:(-4)\\ h&=25 \\ \end{align*}

Tontin pinta-ala on siis suurin silloin, kun tontin rantaa kohti kohtisuora pituus on \(25\) metriä (kuuluu määrittelyjoukkoon). Pinta-ala saadaan nyt funktion\( A(h)\) arvona:

\begin{equation*} A(25)=-2⋅25^2+100⋅25=-2⋅625+2500 \\ = -1250+2500=1250 \:\text{m}^2=12,5 \:\text{aaria}.\end{equation*}