Radiaanit
| Kuva 1 |
|---|
 |
Kulmia on tähän asti merkitty asteina, mutta tämä ei aina ole kovin kätevää.
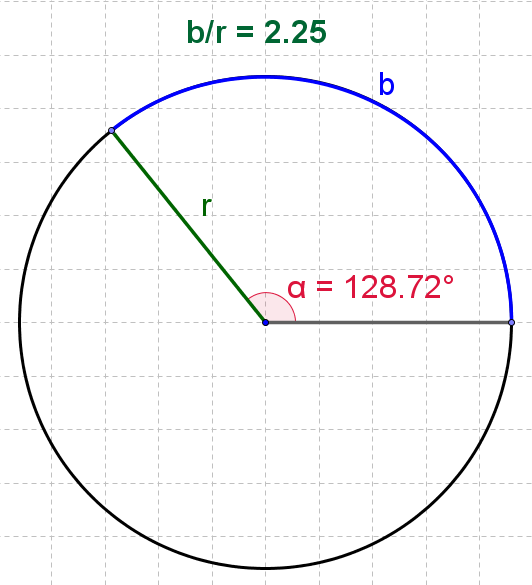
Kulman ilmoittaminen radiaaneina perustuu siihen huomioon, että ympyränkaaren ja säteen pituuksien suhde (ks. kuva 1) pysyy samana riippumatta ympyrän koosta, kun vain kulma α ei muutu. Tästä saadaan seuraava idea:
|
Huomaa, että näin merkiten kulmalla ei ole yksikköä, koska pituuden yksiköt supistuvat jakolaskussa pois. Kulma on radiaaneina pelkkä luku, jonka perään tosin selvyyden vuoksi joskus kirjoitetaan merkintä (rad).
Yllä oleva idea voidaan merkitä lyhyesti seuraavalla tavalla:
| \begin{equation*}α_{\text{rad}}=\frac{b}{r}\end{equation*} |
Kulman \(\alpha \) alaindeksi \(\text{rad}\) viittaa siihen, että kulma on radiaaneina eikä asteina.
Esimerkiksi täyskulman suuruus radiaaneina saadaan jakamalla ympyrän piiri säteellä:
| \(360° = \frac{2\pi r}{r} = 2\pi \) (rad) |
Kuvasta 1 nähdään, että kulmaa \(128,\!72°\) vastaa radiaaneina kulma \(2,\!25\) (kahden desimaalin tarkkuudella).
