\(\renewcommand{\vec}[1]{\mathbf{#1}} \DeclareMathOperator*{\sijoitus}{\Big/} \newcommand{\eval}[2]{\sijoitus_{\kern-0.7em#1}^{\kern0.7em#2}\!} \)
Matematiikka (yläkoulu)
− 1 Luvut ja joukot
− 1.7 Pyöristäminen ja merkitsevät numerot
1.7.3 Pyöristäminen likiarvolaskuissa
+ 2 Prosenttilaskut
+ 3 Yksikönmuunnokset
+ 4 Kirjainlaskenta
+ 5 Geometria
+ 6 Tilastot ja todennäköisyys
7 Pähkinöitä

Pyöristäminen likiarvolaskuissa

Laskuissa pyöristys tehdään vasta lopussa, eli lasketaan mahdollisimman tarkoilla arvoilla mahdollisimman pitkään. Vastauksen pyöristyksessä noudatetaan seuraavia sääntöjä:

Muunna alkuarvot heti alussa samaan yksikköön, jos ne on annettu eri yksiköissä.

Yhteen- ja vähennyslaskut (kun laskussa ei muita laskutoimituksia)
  1. Katso, mikä arvoista on pyöristetty epätarkimmin eli suurimman luvun tarkkuuteen (esim. satojen tarkkuus on epätarkempi kuin kymmenien, ykkösten tai kymmenesosien tarkkuus).
  2. Vastaus pyöristetään samalla tavalla kuin yllä mainittu epätarkin alkuarvo (esimerkiksi kahden desimaalin tarkkuuteen).

Kerto- ja jakolaskut (kun laskussa ainakin yksi kerto- tai jakolasku)
  1. Epätarkin alkuarvo tässä on se alkuarvo, jossa on vähiten merkitseviä numeroita.
  2. Vastaus pyöristetään niin, että siihen jää yhtä monta merkitsevää numeroa kuin on epätarkimmassa alkuarvossa.

Huomaa, että yllä alkuarvolla tarkoitetaan aina likiarvoja eli mittaustuloksia.

Käytännössä jälkimmäinen sääntö on tärkeämpi, koska esimerkiksi fysiikan laskuissa on useimmiten mukana jokin kerto- tai jakolasku.

Esimerkki
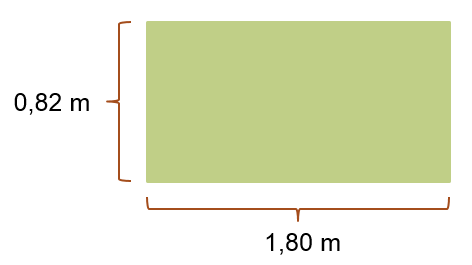
Kuvassa 1 on maton pituudeksi annettu 1,80 m ja leveydeksi 0,82 m.

Ympärysmitta saadaan laskemalla yhteen kaikkien sivujen pituudet:

1,80 m + 1,80 m + 0,82 m + 0,82 m = 5,24 m

Tuloksen tarkkuus on valmiiksi sopiva, koska kysymys on yhteenlaskusta ja kumpikin alkuarvo on annettu sadasosien (senttimetrien) tarkkuudella. Tällöin vastauskin annetaan sadasosien tarkkuudella.

Pinta-ala saadaan kertomalla maton pituus ja leveys keskenään:

1,80 m ⋅ 0,82 m = 1,476 m2 ≈ 1,5 m2

Kysymys on kertolaskusta. Leveydessä 0,82 m on kaksi merkitsevää numeroa, kun taas pituudessa 1,80 m kolme. Vastaus pitää siis pyöristää kahden merkitsevän numeron tarkkuuteen.
Kuva 1

Tänään on lauantai 23.11.2024
Creative Commons -licence Opinnot.net-sivuston sisältöjä saa hyödyntää Creative Commons Attribution-ShareAlike 4.0 International -lisenssin mukaisesti.