Radiaanien ja asteiden suhde

Kuva 1

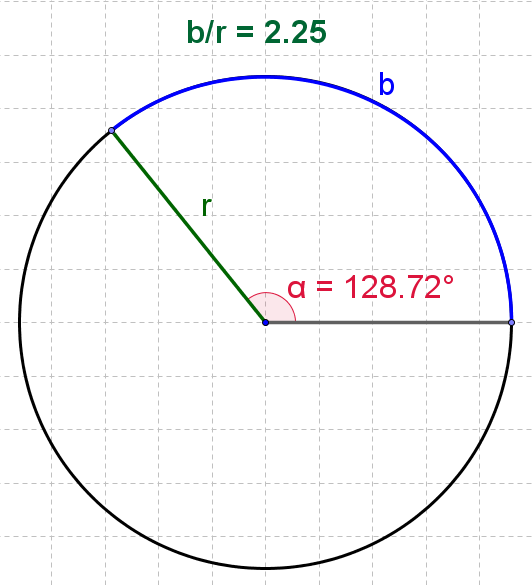Kuva 2

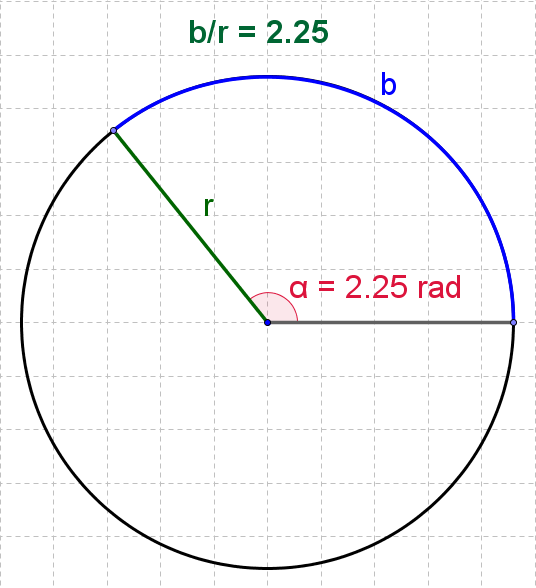Kulman suuruutta joudutaan toisinaan muuttelemaan radiaaneista asteiksi tai toisinpäin.

Kulman \(\alpha\) alaindeksi \(\text{rad}\) viittaa siihen, että kulma on radiaaneina ja alaindeksi \(\text{ast}\) kulmaan asteina.

Edellä esitettiin seuraava merkintä:

\begin{equation*}α_{\text{rad}}=\frac{b}{r}\end{equation*}

Kaaren \(b\) pituus on yhtä suuri osa ympyrän kehästä \((=2πr)\) kuin kulma \(α_{\text{ast}}\) on täyskulmasta \(360°\):

\begin{equation*}b=\frac{α_{\text{ast}}}{360°} \cdot 2πr\end{equation*}

Tämän avulla saadaan yhteys radiaanien \(α_{\text{rad}}\) ja asteiden \(α_{\text{ast}}\) välille:

\(α_{\text{rad}}=\frac{b}{r}=\frac{\frac{α_{\text{ast}}}{360°} \cdot 2πr}{r}\)\(=\frac{α_{\text{ast}}}{360°} \cdot 2π\)

eli

\begin{equation*} α_{\text{rad}}=\frac{α_{\text{ast}}}{360°} \cdot 2π \end{equation*}

Edellistä yhtälöä voidaan kertoa luvulla \(\frac{360°}{2π}\), jolloin saadaan yksikön muunnoskaava toiseen suuntaan (muista murtolukujen kertolasku):

\begin{equation*}α_{\text{ast}}=\frac{α_{\text{rad}}}{2π} \cdot 360°\end{equation*}

Esimerkkejä:

• Jos kulma on asteina \(90\), on se radiaaneina \(α_{\text{rad}}=\frac{90°}{360°} \cdot 2\pi=\frac{1}{4} \cdot 2\pi=\frac{\pi}{2} \: (≈1,57)\)
• Jos kulma on asteina \(360\), on se radiaaneina \(α_{\text{rad}}=\frac{360°}{360°} \cdot 2\pi=2\pi \: (≈6,23)\)
• Jos kulma on asteina noin \(128,72\), on se radiaaneina \(α_{\text{rad}}≈\frac{128,72°}{360°} \cdot 2\pi\: ≈2,25\) (ks. kuva 2).
• Jos kulma on radiaaneina \(\frac{3\pi}{2}\), on se asteina \(α_{\text{ast}}=\frac{\left (\frac{3\pi }{2}\right )}{2π} \cdot 360°= \frac{3\pi }{2} \cdot {\frac{1}{2π}} \cdot 360°= \frac{3}{4} \cdot 360°=270°\)

Huomaa, että radiaanit on tapana ilmoittaa piin \((\pi )\) avulla, jos kulman tarkka asteluku on tiedossa. Tällöin arvo on tarkka (desimaalilukuna saadaan aina vain likiarvo piin takia). Kolmannessa esimerkissä kulma on likiarvo, jolloin piin käyttäminen lopullisessa arvossa ei ole kovin mielekästä.