Määrätty integraali
| Kuva 1 |
|---|
 |
| Kuva 2 |
|---|
 |
| Kuva 3 |
|---|
 |
| Kuva 4 |
|---|
 |
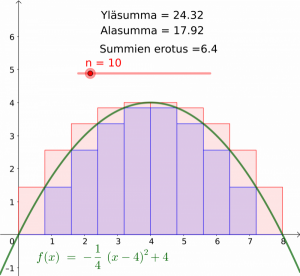
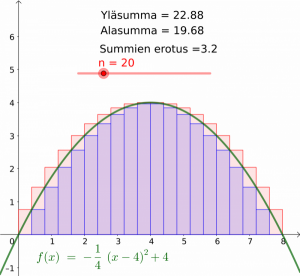
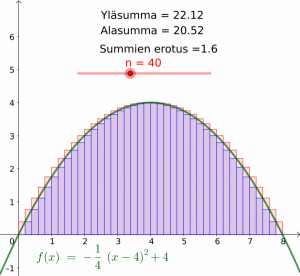
Määrätyn integraalin taustalla on ajatus pinta-alan jakamisesta pienempiin ja pienempiin osiin.
Kuvissa 1-3 on kuvaajan ja \(x\)-akselin välinen alue jaettu suorakulmioihin. Alasumma on kuvaajaan alapuolelta ja yläsumma yläpuolelta rajoittuvien suorakulmioiden pinta-alojen summa. Kun suorakulmioiden lukumäärää (kuvissa \(n\)) suurennetaan rajatta, lähestyvät sekä ylä- että alasumma samaa lukua. Tätä raja-arvoa nimitetään määrätyksi integraaliksi (havainnollistus Geogebralla).
Määrättyä integraalia käytetään esimerkiksi pinta-alojen, tilavuuksien tai käyrän pituuden laskemiseen tai vaikkapa fysiikassa kuljetun matkan laskemiseen nopeuden muuttuessa.
Määrätyssä integraalissa on annettu integroimisrajat ja sen arvo on luku, jonka merkki riippuu funktion arvoista. Jos funktio kulkee \(x\)-akselin alapuolella, saa määrätty integraali negatiivisen arvon (pitää ottaa huomioon pinta-alalaskuissa).
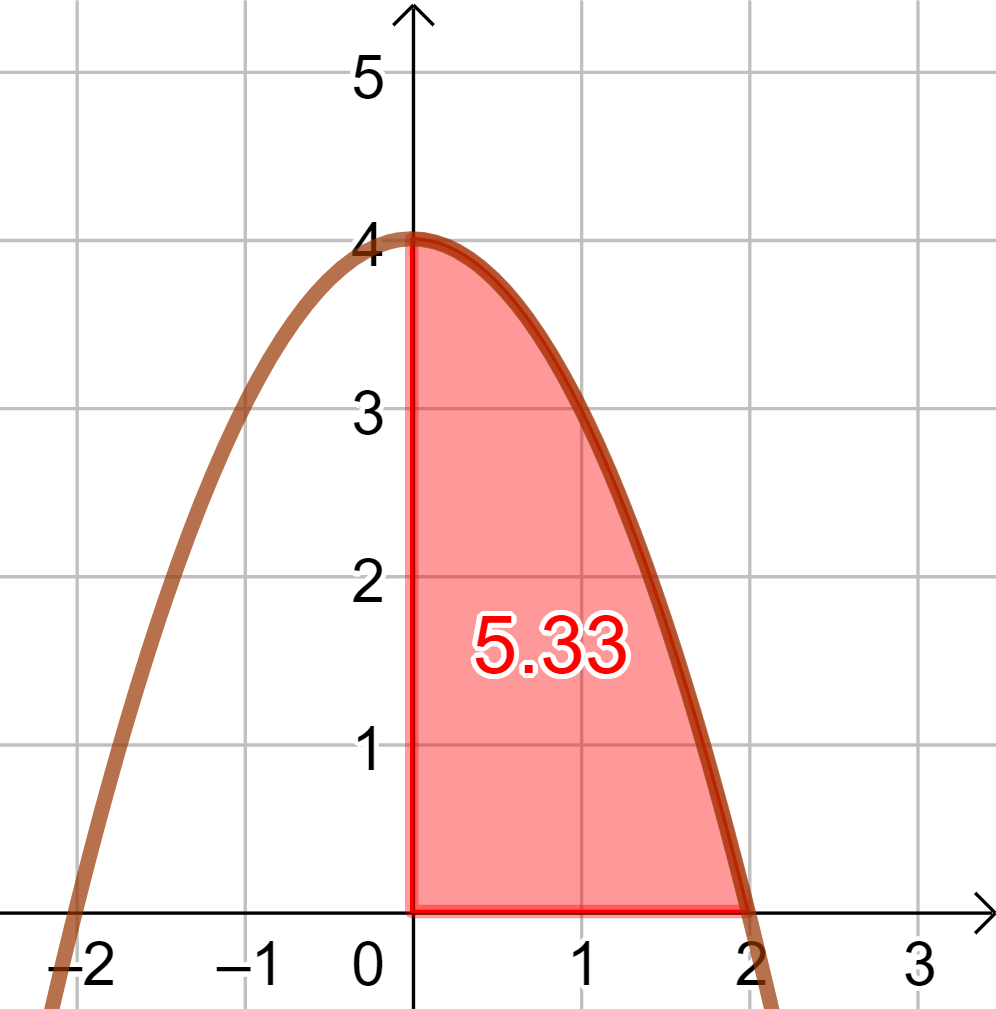
Kuvassa 4 on funktion \(f(x)=-x^2+4\) kuvaaja. Värjätyn alueen pinta-alaa vastaava määrätty integraali merkitään tällöin seuraavasti:
\begin{equation*} A=\int\limits_{0}^{2}f(x) \:\mathrm{d}x=\int\limits_{0}^{2}-x^{2}+4 \:\mathrm{d}x=5\frac{1}{3} \end{equation*}Tulos on tarkka arvo (kuvaan merkitty likiarvo). Huomaa, ettei tästä selviä, miten määrätty integraali on saatu selville. Tuloksen määrittäminen ylä- ja alasumman raja-arvon avulla on hankalaa. Tähän tulee mainioksi avuksi funktion antiderivaatta, vaikka sen yhteys yllä mainittuun raja-arvoon ole lainkaan itsestäänselvä. Analyysin peruslause ilmaisee tämän erittäin tärkeän yhteyden täsmällisesti.
Aina integraalifunktion määrittäminen ei onnistu, jolloin määrätyn integraalin arvo lasketaan numeerisesti. Tällöin vastaus on likiarvo.
Lähteitä ja lisätietoa:
