Analyysin peruslause

Kuva 1

Analyysin peruslause (tai oikeastaan sen seurauslause eli korollaari) antaa tärkeän yhteyden derivaatan ja integraalin välille. Lauseen perusteella määrätyn integraalin arvo välillä \([a, b]\) voidaan määrittää integraalifunktion eli antiderivaatan avulla seuraavasti:

\begin{equation*} \int\limits_{a}^{b}f(x)\:\mathrm{d}x = F(b)-F(a), \end{equation*}

jossa \(F'(x)=f(x)\) ja funktio \(f\) on jatkuva välillä \([a, b]\).

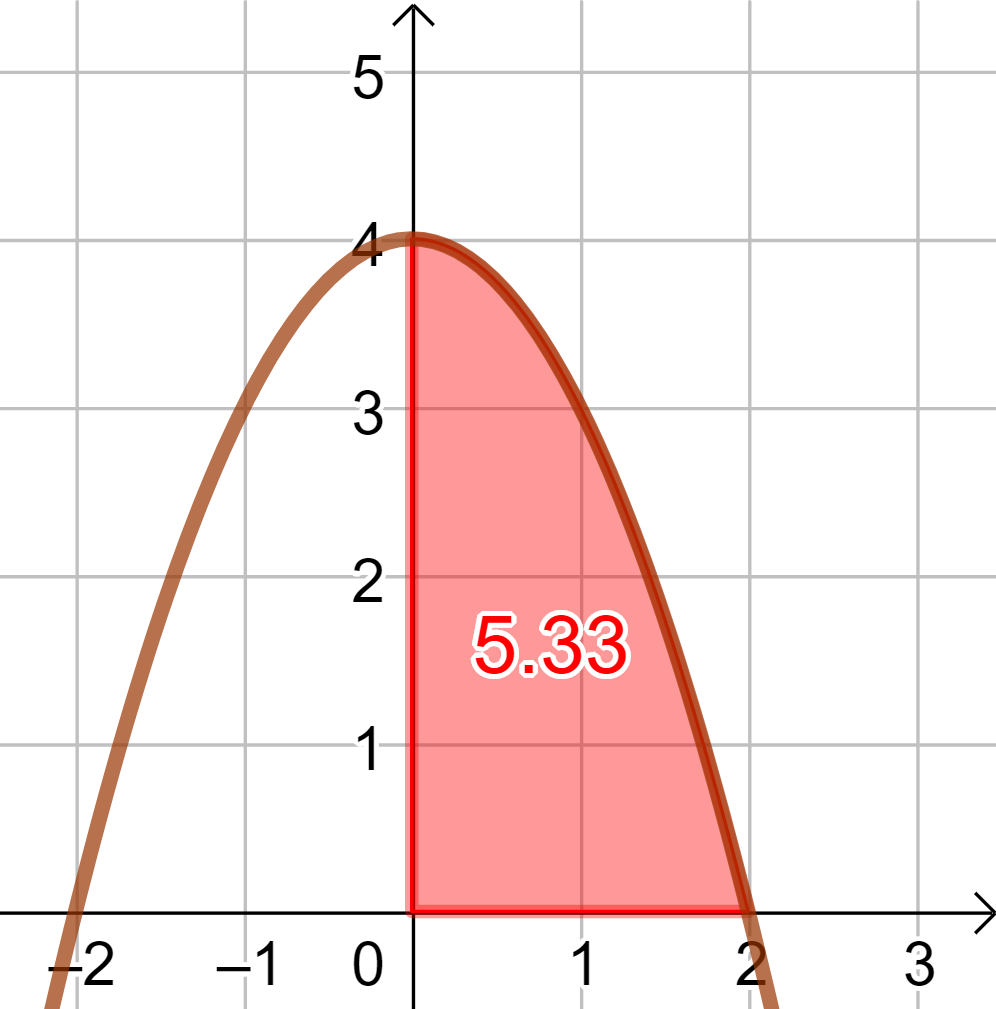
Esimerkki: Kuvassa 1 olevan varjostetun alueen pinta-alan tarkka arvo saadaan määrätyn integraalin arvosta, joka voidaan laskea analyysin peruslauseen antaman idean avulla. Kuvassa on funktion \(f(x)=-x^2+4\) kuvaaja. Olkoon \(F'(x)=f(x)\). Lasku menee seuraavasti:

\begin{align*} A&=\int\limits_{0}^{2}f(x) \:\mathrm{d}x= \int\limits_{0}^{2}\left (-x^{2}+4\right ) \:\mathrm{d}x\\ &=F(2)-F(0)=\left. \left (-\frac{1}{3}x^{3}+4x\right )\right |_0^2\\ &= -\frac{1}{3} \cdot 2^{3}+4 \cdot 2-\left (-\frac{1}{3} \cdot 0^{3}+4 \cdot 0\right )\\ &=-\frac{8}{3}+8=5\frac{1}{3}\\ \end{align*}

Laskussa on hyödynnetty funktion \(f(x)\) antiderivaattaa \(F(x)=\int\limits_{}^{}\left (-x^{2}+4\right ) \:\mathrm{d}x=-\frac{1}{3}x^{3}+4x+C\). Määrätyn integraalin arvo saadaan sijoituksella \(F(2)-F(0)\), joka merkitään usein kuten rivillä 2. Integroimisvakio \(C\in\mathbb{R}\) häviää sijoituksessa aina, joten sitä ei merkitä määrätyn integraalin laskemisessa.