\(\cos(x+y) =\cos x \cos y-\sin x \sin y \)

Kuva 1

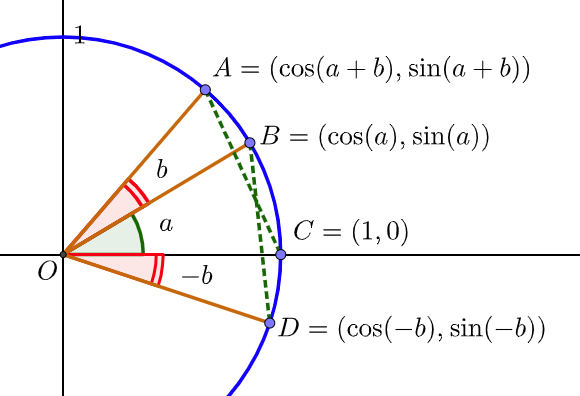Tässä esitetään yksi mahdollinen tapa osoittaa kosinin yhteenlaskukaavan \(\cos(x+y)=\cos x \cos y - \sin x \sin y\) paikkansapitävyys millä tahansa kulmilla \(x\) ja \(y\). Todistus on muunnelma Adamsin (2006) esittämästä todistuksesta Calculus - A Complete Course, Sixth Edition).

Huomaa, että täällä käytetään kulmien arvoina muuttujakirjaimia \(a\) ja \(b\), jotta vältetään sekaannukset koordinaatteihin. Näillä merkinnöillä todistettava kaava on \(\cos(a+b)=\cos a \cos b - \sin a \sin b\).

Kuvan 1 merkinnät ovat olennaisia logiikan ymmärtämiseksi. Tärkeintä on hahmottaa, että kolmiot \(AOC\) ja \(BOD\) ovat aina yhtenevät, eli niiden sivujen pituudet ovat samat. Tämä seuraa siitä, että kummankin kolmion yhtenä kulmana toimii samankokoinen yksikköympyrän keskuskulma \((a+b)\) riippumatta kulmien \(a\) ja \(b\) arvoista. Kolmiot ovat tasakylkisiä (kaksi sivua on ympyrän säteitä), jolloin myös ympyrän kehällä sijaitsevien kantakulmien on pakko olla yhtä suuret kummassakin kolmiossa ja kolmiot ovat näin yhteneviä.

Voit testata täällä, jotta kolmiot pysyvät yhtä suurina millä tahansa kulmilla \(a\) ja \(b\).

Kuvaan on merkitty pisteiden \(A, B, C\) ja \(D\) koordinaatit sinin ja kosinin avulla. Todistuksen lähtökohta on se, että janojen \(AC\) ja \(BD\) pituudet ovat samat, jolloin myös pituuksien neliöt ovat samat (näin päästään heti eroon neliöjuurista).

Muodostetaan janojen pituuksien neliöille lausekkeet kuvan merkintöjen avulla (jana kerrallaan):

Sieventämisessä hyödynnetään tunnettuja yhtäsuuruuksia \((\cos x)^2+(\sin x)^2=1\), \(\cos(-x)=\cos x\) ja \(\sin(-x)=-\sin x\).

\begin{align*} \left |AC\right |^2 &=(\cos(a+b)-1)^2+(\sin(a+b)-0)^2 \\ &=(\cos(a+b))^2-2\cos(a+b)+1+(\sin(a+b))^2 \\ &=(\cos(a+b))^2+(\sin(a+b))^2+1-2\cos(a+b) \\ &=1+1-2\cos(a+b) \\ &=2-2\cos(a+b) \\ \end{align*}

ja

\begin{align*} \left |BD\right |^2 &=(\cos a - \cos (-b))^2+(\sin a - \sin (-b))^2 \\ &=(\cos a - \cos b)^2+(\sin a + \sin b)^2 \\ &=(\cos a)^2 - 2\cos a \cos b+(\cos b)^2+(\sin a)^2 + 2\sin a \sin b + (\sin b)^2 \\ &=(\cos a)^2 +(\cos b)^2+(\sin a)^2 + (\sin b)^2- 2\cos a \cos b+ 2\sin a \sin b \\ &=2 - 2\cos a \cos b+ 2\sin a \sin b \\ \end{align*}

Merkitään nyt pituuksien neliöitä vastaavat lausekkeet yhtä suuriksi ja sievennetään:

\begin{align*} \left |AC\right |^2&=\left |BD\right |^2 \\ 2-2\cos(a+b) &= 2 - 2\cos a \cos b+ 2\sin a \sin b \quad \Vert -2 \\ -2\cos(a+b) &= - 2\cos a \cos b+ 2\sin a \sin b \quad \Vert :(-2) \\ \cos(a+b) &=\cos a \cos b-\sin a \sin b \\ \end{align*}

Ja siinähän se on, haluttu muoto:

\begin{equation*}\cos(a+b) =\cos a \cos b-\sin a \sin b \\ \end{equation*}

jonka muuttujakirjaimet voidaan muuttaa vaikkapa kirjaimiksi \(x\) ja \(y\):

\begin{equation*}\cos(x+y) =\cos x \cos y-\sin x \sin y \\ \end{equation*}