Binomijakauma ja -todennäköisyys

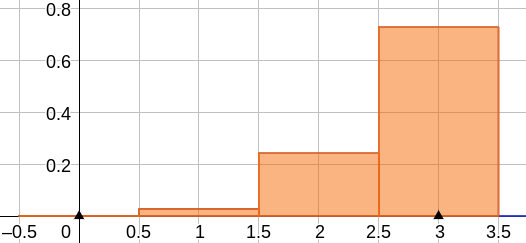
Kuva 1: binomijakauma (maalien todennäköisyydet)

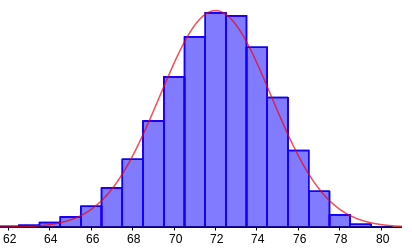
Kuva 2: bin(80, 0.9)

Pekka on jalkapallomaalivahti. Torjuntatilaston mukaan keskimäärin yhdeksän kymmenestä rangaistuspotkusta menee maaliin Pekan ollessa maalivahtina. Millä todennäköisyydellä kolmesta rangaistuspotkusta menee tasan kaksi maaliin?

Merkitään kirjaimella "M" maalia ja kirjaimella "E" ei-maalia (torjunta tai huti). Tässä tapauksessa mahdollisia kahden maalin tulossarjoja on kolme: EMM, MEM ja MME.

Yhden sarjan todennäköisyys saadaan tuloperiaatteen avulla (tapahtumat ovat toisistaan riippumattomia) ja eri sarjojen todennäköisyydet lasketaan yhteen. Maalin todennäköisyys on \(0,9\) ja ei-maalin \(1-0,9 = 0,1\).

\begin{equation*} P(\text{"EMM"}) + P(\text{"MEM"}) + P(\text{"MME"}) \\ = 0,1 \cdot 0,9 \cdot 0,9 + 0,9 \cdot 0,1 \cdot 0,9 + 0,9 \cdot 0,9 \cdot 0,1 \\ = 3 \cdot 0,9 \cdot 0,9 \cdot 0,1 = 0,243 \end{equation*}

Tulos on selvillä, mutta mielenkiintoiseksi laskun tekee seuraava muokkaus:

\begin{equation*} 3 \cdot 0,9 \cdot 0,9 \cdot 0,1 \\ =\binom{3}{2}0,9^{2}(1-0,9)^{3-2} \end{equation*}

Yllä nimittäin ainoat tarvittavat tiedot ovat maalien lkm (2), potkujen lkm (3) ja maalin todennäköisyys (0,9).

Toistokoe yleisesti (riippumattomat tapahtumat): Todennäköisyys sille, että toivottu tulos tulee \(k\) kertaa silloin, kun koetta toistetaan \(n\) kertaa, on seuraava:

\begin{equation*} P(X=k) = \binom{n}{k}p^{k}(1-p)^{n-k} \end{equation*}

Kaavassa \(p\) on todennäköisyys sille, että yksittäisessä kokeessa (ks. Bernoullin koe) tulee toivottu tulos.

Kirjaimella \(X\) merkitään satunnaismuuttujaa, jonka arvo (tässä \(k\)) kertoo, kuinka monesti toivottu tulos sattuu.

Binomijakauma saadaan, kun selvitetään todennäköisyydet kaikilla mahdollisilla muuttujan \(k\) arvoilla \(0, 1, ..., n\). Kuvassa 1 on jalkapalloesimerkin binomijakauman kuvaaja, jossa kutakin todennäköisyyttä vastaa yhden levyinen palkki, jolloin todennäköisyyden arvo on sama kuin palkin pinta-ala. Palkin keskellä on aina varsinainen muuttujan \(k\) arvo (kokonaisluku).Tämä esitys on näppärä, kun verrataan binomijakaumaa ja siihen liittyviä todennäköisyyksiä normaalijakaumaan.

Binomijakaumaa merkitään \(\text{bin}\left (n, p\right )\).

Binomijakauman odotusarvo \(\mu\) ja keskihajonta \(\sigma\) saadaan seuraavasti:

\begin{align*} \mu&=np \\ \sigma&=\sqrt{np(1-p)} \end{align*}

Kun toistokertojen lukumäärä kasvaa, alkaa jakauma muistuttaa normaalijakaumaa. Kuvassa 2 on maalien todennäköisyyksien jakauma silloin kun toistoja on 80. Kuvaan on piirretty punaisella normaalijakauman kuvaaja.