Toisen asteen polynomifunktion kuvaaja

Kuva 1

Toisen asteen polynomifunktion \begin{equation*}f(x)=ax^2+bx+c \end{equation*} kuvaaja on paraabeli. Paraabelin jokaisessa pisteessä etäisyys polttopisteeseen ja johtosuoraan on yhtä suuri (tarkempi selitys).

Paraabelin symmetrisesti puolittava suora on nimeltään akseli (kuvan tapauksessa y-akseli). Huipuksi puolestaan nimitetään paraabelin ja akselin leikkauspistettä.

Funktio voidaan aina kirjoittaa muotoon \begin{equation*}f(x)=a(x-x_0)^2+f(x_0),\end{equation*} jolloin paraabelin huippu on pisteessä \((x_0, f(x_0))\).

Paraabelin aukeamissuunnan määrää kertoimen \(a\) etumerkki. Suunta on ylös, kun \(a > 0\) ja alas, kun \(a < 0\). Jos \(a=0\), ei kuvaaja ole paraabeli, vaan suora.

Vakiotermi vaikuttaa vain kuvaajan pystysuoraan sijaintiin.

Kertoimen \(a\) suuruus vaikuttaa erityisesti paraabelin leveyteen. Mitä suurempi on kertoimen itseisarvo, sitä kapeampi on paraabeli, ja päinvastoin.

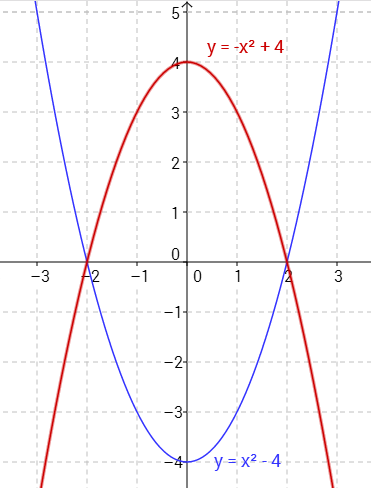
Kuvassa 2 ylöspäin aukeavan paraabelin yhtälö on \(y=x^2-4\), kun taas alaspäin aukeavan \(y=-x^2+4\).

(Suoran) paraabelin huippu on aina nollakohtien keskipisteen kohdalla (jos paraabelilla on nollakohtia). Nollakohdat saadaan toisen asteen yhtälöstä, joka syntyy, kun funktion arvo merkitään nollaksi.

Huipun \(x\)-koordinaatti saadaan myös suoraan toisen asteen yhtälön ratkaisukaavasta jättämällä siitä pois neliöjuuritermi:

\begin{equation*} x_{\text{huippu}}=\frac{-b}{2a} \end{equation*}

Yllä mainittu toimii jopa niissä tapauksissa, joissa yhtälöllä ei ole ratkaisuja, eli juurrettava on negatiivinen (!).