Eksponenttifunktion määrittely- ja arvojoukko

Kuva 1

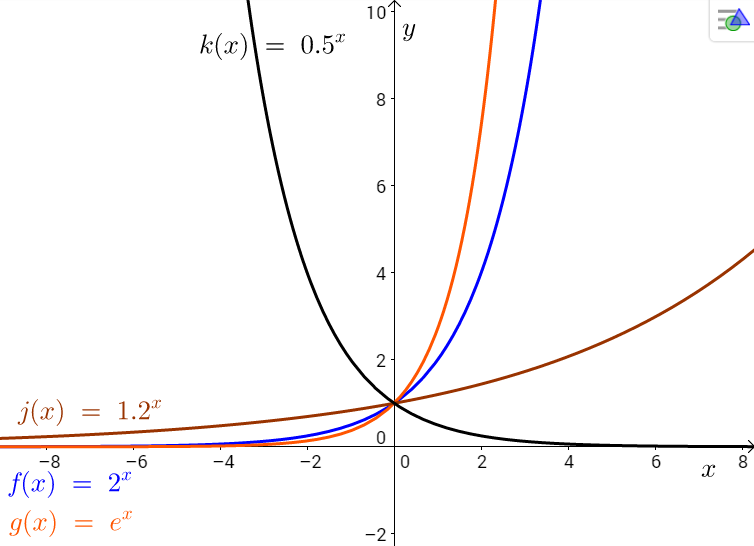Eksponenttifunktio on muotoa \(f(x)=a^x\), jossa kantaluku \(a\) on positiivinen reaaliluku, mutta ei yksi (tällöin funktio olisi vähän tylsä, koska saisi aina arvon 1).

Määrittelyjoukko

Eksponentti \(x\) voi olla mikä vain, joten funktion määrittelyjoukko on koko reaalilukujen joukko \(\mathbb{R}\) (potenssi voidaan määritellä myös irrationaalilukueksponenteille).

Arvojoukko

Koska on sovittu, että kantaluku a on positiivinen, on myös potenssin arvo aina positiivinen. Toisin sanoen funktion \(f\) arvojoukko on positiivisten reaalilukujen joukko \(\mathbb{R}_+\).

Merkintä

Yllä olevat seikat voidaan merkitä ytimekkäästi seuraavalla merkinnällä: \begin{equation*}f: \mathbb{R}\to \mathbb{R}_+\end{equation*}