Binomijakauman normaaliapproksimaatio

Kuva 1: binomijakauma

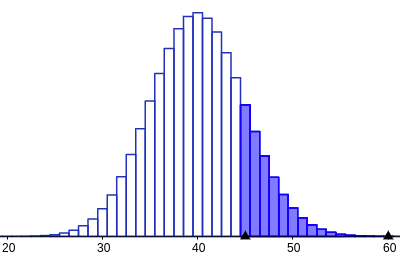Kuva 2: normaalijakauma

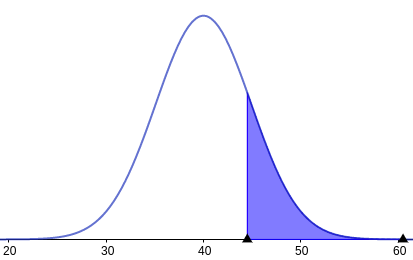Kun toistokokeen toistomäärä kasvaa, alkaa binomijakauma eli binomitodennäköisyydet muuttujan \(k\) arvoilla \(0, 1, \text{...} ,n\) muistuttaa enemmän ja enemmän normaalijakaumaa. Kuvassa 1 on kuvaaja binomijakaumasta arvoilla ja \(n = 100\) ja \(p=0,\!4\), ja kuvassa 2 normaalijakauma arvoilla \(\mu=40\) ja \(\sigma = 4,\!90\).

Binomijakauman odotusarvo \(\mu\) ja keskihajonta \(\sigma\) saadaan seuraavasti:

\begin{align*} \mu&=np \\ \sigma&=\sqrt{np(1-p)} \end{align*}

Esimerkki:

Ella harrasti jousiammuntaa ja osui kaukana olevaan maalitauluun 40 prosentin todennäköisyydellä. Hän ampui 100 nuolta. Millä todennäköisyydellä hän osui tauluun 45-60 kertaa? Oletetaan, ettei väsymys tms. tekijät vaikuttaneet osumistodennäköisyyteen.

Binomitodennäköisyyden mukaan kysytty todennäköisyys on

\begin{equation*}P(k=45) + P(k=46) + ... + P(k=60), \end{equation*}

jossa lasketaan erikseen jokaista suotuista muuttujan \(k\) arvoa vastaava todennäköisyys .

Laskin antaa tulokseksi noin \(0,1789\).

Approksimoidaan sama normaalijakauman avulla: \(\mu=np=100 \cdot 0,4=40\) ja \(\sigma=\sqrt{np(1-p)}=\sqrt{40\cdot0,6}\approx 4,8990 \).

\begin{equation*} P(45 \leq k \leq 60 ) \approx P(44,\!5 \leq X \leq 60,\!5 ) \approx 0,1791 \end{equation*}

Yllä kirjain \(X\) viittaa normaalijakaumaa noudattavaan satunnaismuuttujaan. Välin päätepisteille on tehty ns. jatkuvuuskorjaus, jonka avulla normaalijakauma vastaa paremmin binomijakaumaa erityisesti pienillä toistokertojen \(n\) määrällä. Huomataan, että normaalijakauman avulla saatu tulos on erittäin lähellä binomijakauman tulosta (kolmen merkitsevän numeron tarkkuudella sama).

Kuvissa kysyttyä todennäköisyyttä vastaa varjostetun alueen pinta-ala, joka silmämääräisestikin vaikuttaa suunnilleen samankokoiselta.