Normaalijakauma

Kuva 1

Kuva 2

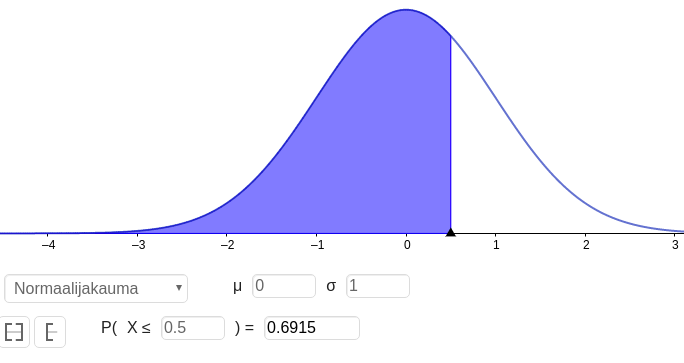Normaalijakauma on eräs jatkuva todennäköisyysjakauma, jonka tiheysfunktion kuvaajan muoto muistuttaa kirkonkellon profiilia (tästä nimitys Gaussin kellokäyrä kehittäjänsä Carl Friedrich Gaussin mukaan, ks. kuva 1).

Jatkuvan satunnaismuuttujan \(X\) tiheysfunktio, jossa \(x\) on satunnaismuuttujan arvo, \(\mu\) odotusarvo (keskiarvo) ja \(\sigma\) keskihajonta:

\begin{equation*}f(x) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\end{equation*}

Huomautus: toisinaan funktio kirjoitetaan muodossa \(f_X(x)\), kun halutaan korostaa satunnaismuuttujaa.

Jos muuttujan arvojen \(x\) jakauma (tiheysfunktion kuvaaja) on Gaussin kellokäyrän muotoinen, noudattaa muuttuja normaalijakaumaa. Tämä voidaan merkitä lyhyesti

\begin{equation*}X\sim \operatorname{N}(\mu,\sigma),\end{equation*}

jossa \(\mu\) on odotusarvo ja \(\sigma\) keskihajonta. Sanottuna "satunnaismuuttuja \(X\) noudattaa normaalijakaumaa, jonka odotusarvo on myy ja keskihajonta sigma".

Normitettu normaalijakauma: odotusarvo (keskiarvo) \(\mu = 0 \) ja keskihajonta \(\sigma=1\) (jolloin myös varianssi \(\sigma^2=1\)). Tällöin \(X\sim \operatorname{N}(0,1)\) ja vastaava tiheysfunktio on seuraava:

\begin{equation*}f(x) = \frac{1}{\sqrt{2 \pi}} e^{-x^2/2}\end{equation*}

Kertymäfunktio \(\Phi(x)\) (lue fii):

\begin{equation*} \Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-t^2/2} \, dt, \end{equation*}

\(\Phi(x)\) antaa todennäköisyyden tapaukselle "satunnaismuuttujan \(X\) arvo on pienempi tai yhtä suuri kuin \(x\)" eli lyhyesti \(P(X \leq x)\). Geometrisesta tulkittuna tämä vastaa tiheysfunktion ja \(x\)-akselin väliin jäävän alueen pinta-alaa. Edellytyksenä tässä on, että satunnaismuuttuja noudattaa normitettua normaalijakaumaa.

Kuvassa 1 on tiheysmuuttujien kuvaajat, joista matalampi on normitetulle jakaumalle ja toinen ei-normitetulle jakaumalle, jonka keskihajonta on \(0,\!3\).

Kuvassa 2 on kertymafunktion \(\Phi(0,\!5)\) arvon havainnollistus. Kuvassa on varjostettu alue, jonka pinta-ala vastaa todennäköisyyttä \(P(X\leq 0,\!5)\).

Huom: usein normitettuun satunnaismuuttujaan viitataan kirjaimella \(Z\) ja vastaavasti muuttujan arvoon kirjaimella \(z\).