Rasiakuvaajat (Ti-nspire)

Kuva 1

Kuva 2

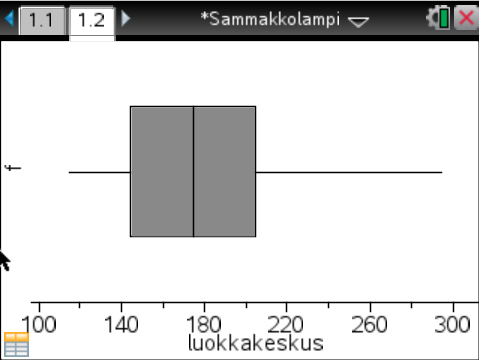
Rasiakuvaaja on tilastollinen kuvaaja, jossa suorakulmion reunat näyttävät tilaston ala- ja yläkvartiilin arvon (Q₁ ja Q₃). Suorakulmion sisällä on pystyviiva, joka osoittaa mediaanin arvon (Q₂).

Rasiakuvaajan ”viiksien” pituudet voidaan piirtää eri tavoilla:

Menetelmä 1: yksinkertaisimmassa menetelmässä viikset ulottuvat aina tilaston pienimpään ja suurimpaan arvoon.

Menetelmä 2: menetelmä (jota esimerkiksi TI-inspire käyttää) on rajoittaa viiksien pituudet niin, että viiksi alaspäin / vasemmalle ulottuu pienimpään arvoon, joka on korkeintaan 1,5 kvartiilivälin pituuden (Q₃ − Q₁) päässä alakvartiilista. Vastaavasti viiksi ylöspäin / oikealle ulottuu suurimpaan arvoon, joka on korkeintaan 1,5 kvartiilivälin pituuden päässä yläkvartiilista. Viiksien ulkopuolella mahdollisesti jäävät arvot merkitään pisteinä.

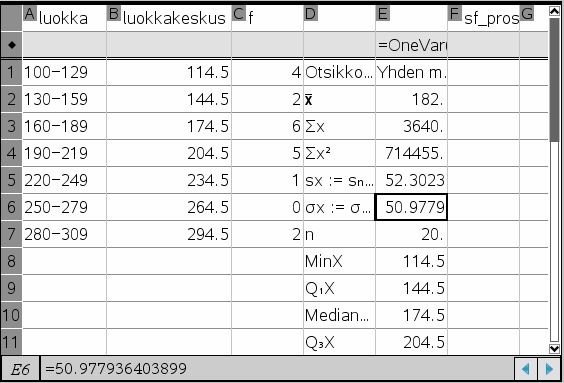
Kuvassa 1 on TI-nspire-laskimella tehty rasiakuvaaja ja siihen liittyvät arvot näkyvät kuvassa 2. Kyseisessä tapauksessa tilasto on luokiteltu, jolloin kutakin luokkaa vastaavana likiarvona käytetään luokkakeskusta. Viiksien ulkopuolelle ei tässä tapauksessa jää arvoja.

Huom: TI-nspire halusi (2018) välttämättä merkitä frekvenssisarakkeen nimen ikäänkuin pystyakselille, vaikkei rasiakuvaajassa pystyakselia olekaan (kuvassa 1). Tämä ominaisuus on korjattu uudemmissa versioissa.

Laskinohje (Tinspire): Tarkemman ohjeen löydät seuraavasta linkistä:

www.opinnot.net/kokonaisuudet/index.php?id_kokon=223