Kvartiilit frekvenssitaulukosta
Jos tilastossa on eri arvoja rajoitettu määrä, voidaan frekvenssitaulukossa antaa kaikki erilliset arvot ja niitä vastaavat frekvenssit. Usein mahdollisia arvoja on kuitenkin liikaa tai jopa äärettömästi (jatkuva muuttuja), jolloin frekvenssitaulukossa käytetään luokittelua, eli annetaan välit, joilla arvot sijaitsevat. Seuraavassa ohjeet kvartiilien määrittämiseen kummassakin tapauksessa:
| Määritysohje: frekvenssitaulukko - yksittäiset arvot |
|---|
1) Laske arvoille suhteelliset summafrekvenssit (merkitään sf (%)). 2) Alakvartiili on ensimmäinen arvo, jonka sf (%) on vähintään* 25 %. 3) Mediaani on ensimmäinen arvo, jonka sf (%) on vähintään* 50 %. 4) Yläkvartiililuokka on ensimmäinen arvo, jonka sf (%) on vähintään* 75 %. * Huomaa: jos sf (%) on täsmälleen 25, 50 tai 75 %, ks. selitys alla! |
| Määritysohje: frekvenssitaulukko - luokiteltu aineisto |
|---|
1) Laske luokille luokkakeskukset ja suhteelliset summafrekvenssit (merkitään sf (%)). 2) Alakvartiililuokka on ensimmäinen luokka, jonka sf (%) on vähintään* 25 %. 3) Mediaaniluokka on ensimmäinen luokka, jonka sf (%) on vähintään* 50 %. 4) Yläkvartiililuokka on ensimmäinen luokka, jonka sf (%) on vähintään* 75 %. 5) Ala- ja yläkvartiilin sekä mediaanin arvo on vastaavan luokan luokkakeskus. * Huomaa: jos sf (%) on täsmälleen 25, 50 tai 75 %, ks. selitys alla! |
* Huomautus: jos yllä sf (%) on täsmälleen 25, 50 tai 75 % ja mediaania määritetään parillisesta määrästä arvoja, viittaa suhteellisen summafrekvenssin kyseinen arvo siihen, että keskimmäiset kaksi arvoa ovat taulukossa eri riveillä! Tällöin mediaani saadaan näiden arvojen keskiarvona. Käytännössä tähän törmätään aika harvoin, mutta harjoitustehtävissä voi tulla vastaan.
Esimerkki 1 (luokiteltu aineisto)
| Kuva 1: Frekvenssitaulukko |
|---|
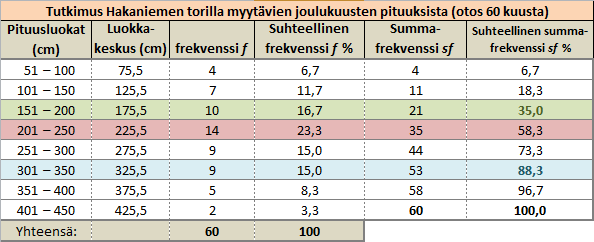 |
1) Taulukossa laskettu luokkakeskukset ja suhteelliset summafrekvenssit (sf %).
2) Alakvartiililuokka on luokka 151–200 (vihreä), jonka sf (%) on ensimmäisenä vähintään 25 %.
3) Mediaaniluokka on luokka 201–250 (punertava), jonka sf (%) on ensimmäisenä vähintään 50 %.
4) Yläkvartiililuokka on luokka 301–350 (sininen), jonka sf (%) on ensimmäisenä vähintään 75 %.
5) Ala- ja yläkvartiilin sekä mediaanin likiarvona voidaan pitää kyseisen luokan luokkakeskusta, jolloin alakvartiiliksi saadaan 175,5 cm, mediaaniksi 225,5 cm ja yläkvartiiliksi 325,5 cm. Kvartiilivälin pituus on tällöin noin 325,5 cm – 175,5 cm = 150 cm.
