Yhteenlaskusääntö

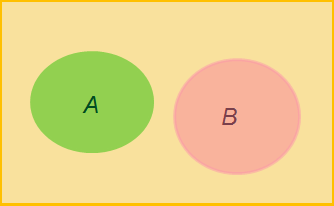
Kun tapahtumat \(A\) ja \(B\) ovat erillisiä (ei yhteisiä alkeistapauksia), lasketaan tapahtuman "joko \(A\) tai \(B\)" todennäköisyys yksittäisten todennäköisyyksien summana.

Huomaa, että joukko-opin näkökulmasta merkintää \(A \:\text{tai}\: B\) vastaa merkintä \(A\cup B\) ja samoin merkintää \(A \:\text{ja}\: B\) vastaa merkintä \(A\cap B\).

\(P(A \:\text{tai}\: B) =\) \(P(A) + P(B) \) eli \(P(A\cup B) =\) \(P(A) + P(B)\)

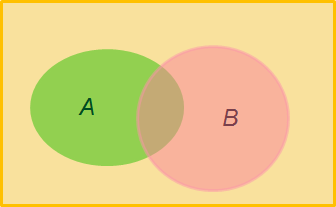
Jos joukot \(A\) ja \(B\) eivät ole erillisiä, lasketaan todennäköisyys seuraavasti:

\(P(A \:\text{tai}\: B) =\) \(P(A) + P(B) − P(A \:\text{ja}\: B)\) eli \(P(A\cup B) =\) \(P(A) + P(B) − P(A \cap B)\)

Esimerkki erillisistä tapahtumista:

Noppaa heitettäessä tapahtumat "saada ykkönen" ja "saada kakkonen" ovat erillisiä tapahtumia. Tällöin tapahtuman "saada ykkönen TAI kakkonen" todennäköisyys lasketaan kaavalla \(P(\:\text{"saada ykkönen"}) +P(\:\text{"saada kakkonen"})=\) \(\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\).

Esimerkki ei-erillisistä tapahtumista:

Noppaa heitettäessä tapahtumat "saada parillinen luku" ja "saada vähintään viitonen" eivät ole erillisiä, koska silmäluku kuusi sopii kumpaankin. Merkitään suotuisten silmälukujen (alkeistapausten) joukkoja seuraavasti:

• \(A=\{2,4,6\}\) tapahtumassa "saada parillinen luku"
• \(B=\{5,6\}\) tapahtumassa "saada vähintään viitonen"
• \(A \:\text{ja}\: B = A\cap B=\{6\}\)

Merkintöjen avulla voidaan laskea tapahtuman "saada parillinen luku TAI vähintään viitonen" todennäköisyys seuraavasti:

\(P(A \:\text{tai}\: B) = P(A)+P(B)-P(A \:\text{ja}\: B)=\) \(\frac{3}{6}+\frac{2}{6}-\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)

Samaan tulokseen päästään myös laskemalla suotuisten tapausten {2,4,5,6} lukumäärä ja jaetaan se kaikilla eli kuudella.