Paraabeli

Kuva 1

Kuva 2

Toisen asteen polynomifunktion \(f(x)=ax^2+bx+c\) kuvaaja on paraabeli. Paraabelin jokaisessa pisteessä etäisyys polttopisteeseen ja johtosuoraan on yhtä suuri. Paraabelin symmetrisesti puolittava suora on nimeltään akseli. Huipuksi puolestaan nimitetään paraabelin ja akselin leikkauspistettä.

Kuvassa 1 paraabelin olennaiset osat menevät seuraavasti:

• paraabeli - sininen viiva
• paraabelin huippu - piste D
• polttopiste - piste A
• johtosuora - suora \(y=1\) (vihreä)
• akseli - pystysuora suora \(x=1\)
• paraabelin pisteen etäisyys polttopisteestä - janan AB pituus (\(= h\))
• paraabelin pisteen etäisyys johtosuorasta - janan BC pituus (\(= j\))
• polttopisteen ja huipun välinen etäisyys \(=p\)
• huipun ja johtosuoran välinen etäisyys \(=p\)

Paraabelin yhtälömuoto voidaan kirjoittaa seuraavasti, kun akseli on pystysuora: \begin{equation}y-y_0=a(x-x_0)^2\:,\end{equation} missä \(a=\frac{1}{4p}\) ja pisteessä \((x_0,y_0)\) on paraabelin huippu.

Funktiomuodossa sama tulee seuraavasti: \begin{equation}f(x)-f(x_0)=a(x-x_0)^2\:,\end{equation} missä vastaavasti \(a=\frac{1}{4p}\) ja huippu \((x_0,f(x_0))\).

Paraabelin aukeamissuunnan määrää kertoimen \(a\) etumerkki.

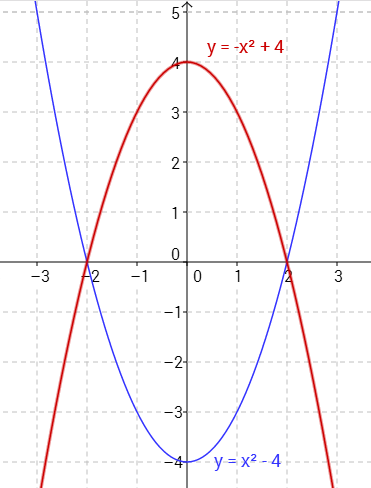
Kuvassa 2 ylöspäin aukeavan paraabelin yhtälö on \(y=x^2-4\), kun taas alaspäin aukeavan \(y=-x^2+4\).

Vakiotermi vaikuttaa vain kuvaajan pystysuoraan sijaintiin.

Kertoimen \(a\) suuruus vaikuttaa paraabelin leveyteen. Mitä suurempi on kertoimen itseisarvo, sitä kapeampi on paraabeli, ja päinvastoin.

Huomaa, että etäisyydeksi \(p\) saadaan negatiivinen luku, kun \(a<0\). Tämä viittaa siihen, että polttopiste on huippua alempana. Olisikin tarkempaa sanoa, että arvo \(p\) on polttopisteen \(y\)-koordinaatti miinus huipun \(y\)-koordinaatti. Tällöin paraabeli menee aina oikein päin (kun puhutaan paraabeleista, joiden akseli on pystysuora).