Yhtälö
| Kuva 1 |
|---|
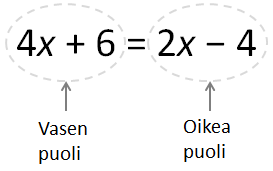 |
Yhtälö saadaan, kun kaksi matemaattista lauseketta merkitään yhtä suuriksi.
Yhtälöitä ovat esimerkiksi seuraavat:
\(2x + 7 = 3\)
\(2x^{3} + 7 = \frac{−x + 3}{2x}\)
\(x + y + z = 0\)
Muuttujan korkein potenssi antaa yhtälön asteen.
| Yhtälö ratkaistaan hakemalla tuntemattomalle sellainen arvo, jolla yhtälön puolet ovat yhtä suuria. Tämä arvo on yhtälön ratkaisu eli juuri. |
Yhtälöllä on korkeintaan yhtälön asteluvun verran juuria (esimerkiksi toisen asteen yhtälöllä on 0, 1 tai 2 juurta reaalilukujen joukossa).
Esimerkki: yhtälön \(4x − 4 = x − 1\) ratkaisu on \(x = 1\), koska tällöin yhtälön vasen puoli \(\mathbf{4x − 4} = 4 · 1 − 4 = 0\) ja yhtälön oikea puoli \(\mathbf{x − 1} = 1 − 1 = 0\) ovat yhtä suuria (kummankin arvo on nolla).
Yhtälön ratkaiseminen:
Tavoite: muokata yhtälöä niin, että tuntematon jää yksin yhtälön toiselle puolelle, jolloin yhtälön mahdollinen ratkaisu nähdään suoraan (esim. \(x = 2\)).
Keinot: yhtälöä saa muokata erilaisilla laskutoimituksilla, kun vain yhtälön molemmille puolille tehdään samat toimenpiteet. Älä kuitenkaan kerro nollalla!
Yhtälön perusteet voit kerrata tarkemmin vaikkapa täällä.
