Toisen asteen yhtälö

Kuva 1: yleinen muoto

Kuva 2: ratkaisukaava

Toisen asteen yhtälön puolet ovat polynomeja, joista korkeamman (tai kummankin) aste on 2. Toisin sanoen muuttujan korkein potenssi on 2.

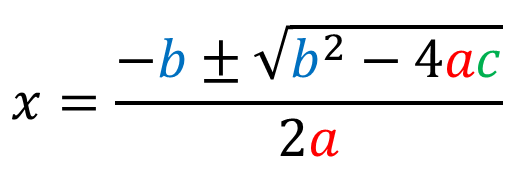Yhden muuttujan toisen asteen yhtälön yleinen muoto on seuraava:

ax2 + bx + c = 0

Kaavassa vakiot \(a\neq 0\), \(b\) ja \(c\) ovat reaalilukuja. Luvut \(b\) ja \(c\) voivat olla nollia, mutta \(a\) ei saa olla nolla (tällöin kyseessä ei ole toisen asteen yhtälö).

Toisen asteen yhtälöllä on nolla, yksi tai kaksi ratkaisua (reaalilukujen joukossa), jotka saadaan selville ratkaisukaavan (kuvassa 2) avulla.

Esimerkki:

Yhtälössä \(x^{2}+x-6=0\) vakiota \(a\) vastaa luku \(1\), vakiota \(b\) luku \(1\) ja vakiota \(c\) luku \(-6\). Yhtälön ratkaisu saadaan ratkaisukaavaan sijoittamalla seuraavasti:

\begin{equation} x=\frac{-1\pm \sqrt{1^{2}-4 \cdot 1 \cdot \left (-6\right )}}{2 \cdot 1} =\frac{-1\pm \sqrt{1+24}}{2} =\frac{-1\pm 5}{2} \end{equation}

Tulokseksi saadaan, että tuntemattomalla on kaksi eri arvoa. Lasketaan ne erikseen:

\(x=\frac{-1+ 5}{2}=\frac{4}{2}=2\) tai \(x=\frac{-1- 5}{2}=\frac{-6}{2}=-3\)

Ratkaisu: \(x = 2\) tai \(x=-3\). Sijoittamalla arvot alkuperäiseen yhtälöön huomataan, että kummallakin arvolla yhtälön puolista tulee samat luvut (nolla). Ratkaisut ovat siis oikeita.