Rationaalifunktion nollakohdat
| Kuva 1 |
|---|
 |
Rationaalifunktion nollakohdat ovat ne osoittajan nollakohdat, jotka kuuluvat funktion määrittelyjoukkoon.
Jos osoittajan nollakohta on myös nimittäjän nollakohta, ei sitä oteta mukaan, koska tällöin funktion arvo ei ole määritelty (nimittäjän nollakohta ei kuulu määrittelyjoukkoon)!
Funktiossa
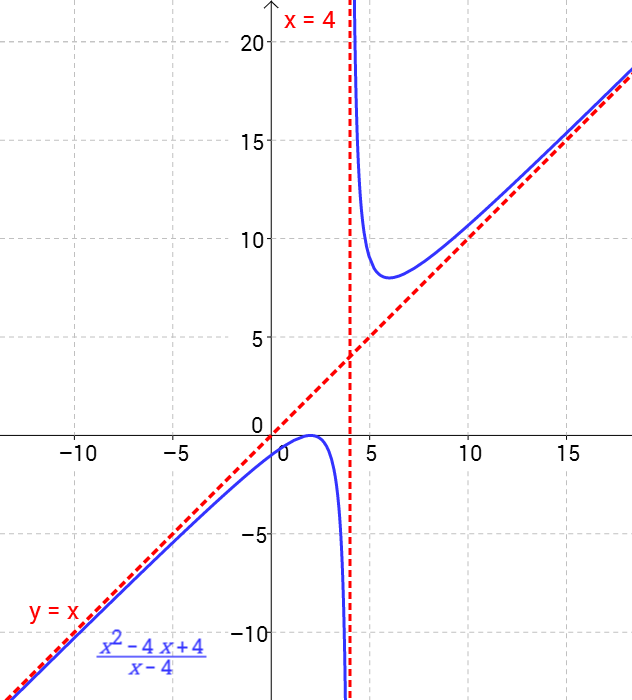
\begin{equation*} R(x)=\frac{x^{2}-4x+4}{x-4 } \end{equation*}osoittajan eli polynomin \(x^2−4x + 4\) nollakohdat saadaan ratkaisemalla yhtälö \(x^2−4x + 4=0\) toisen asteen yhtälön ratkaisukaavalla:
\begin{equation*} x=\frac{-b\pm \sqrt{b^2-4ac}}{2a} =\frac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot1}\\ =\frac{4\pm \sqrt{16-16}}{2} =\frac{4\pm \sqrt{0}}{2}=2 \end{equation*}Ratkaisuja on yksi, \(x = 2\), joka kuuluu funktion määrittelyjoukkoon (nimittäjän nollakohta on \(4\), joten siitä ei tule ongelmaa).
Kuvasta 1 nähdään, että kuvaaja (kaksiosainen sininen yhtenäinen viiva) käy kerran \(x\)-akselilla.
