Tangentin yhtälö

Kuva 1

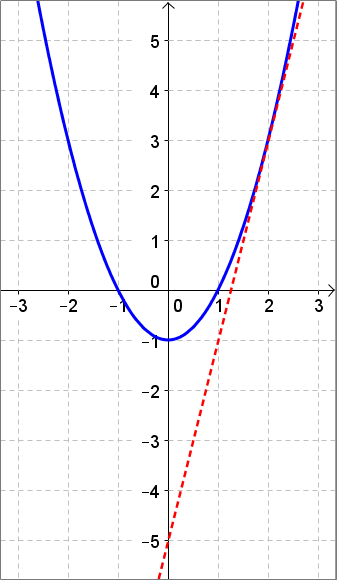Olkoon funktio \(f(x)=x^2−1\). Mikä on funktiolle kohtaan \(x=2\) piirretyn tangentin yhtälö?

Ratkaisu: tangentti on suora, jonka yhtälö on yleensä muotoa \(y=kx+b\). Kulmakerroin \(k\) on sama kuin funktion \(f \) derivaatta kohdassa \(x=2\):

\(f′(x)=2x\), jolloin \(f′(2)=2⋅2=4 = k\).

Tangentin yhtälö on siis tässä tapauksessa muotoa \(y=4x+b\). Vakiotermi \(b\) saadaan selville seuraavasti:

Tapa 1

Tangentti hipaisee funktiota kohdassa \(x=2\), jolloin pisteen \(y\)-koordinaatti on \(f(2)=2^{2}−1=3\). Toisin sanoen tangentti kulkee pisteen \((2,3)\) kautta. Sijoitetaan arvot eli \(x=2\) ja \(y=3\):

\begin{align*} y&=4x+b \\ 3&=4⋅2+b \\ 3&=8+b \quad \Vert −8 \\ -5&=b \\ b&=−5 \end{align*}

Nyt kaikki tarvittava on tehty. Tangentin yhtälö on siis \(y=4x−5\).

Tapa 2

Toinen tapa on käyttää suoran yhtälön muotoa

\begin{equation*}y-y_0=k(x-x_0), \end{equation*}

johon tunnetun pisteen \((x_0, y_0) = (2,3)\) koordinaatit sekä kulmakertoimen \(k\) arvon voi sijoittaa suoraan:

\begin{align*} y-3&=4(x-2) \\ y-3&=4x-8 \quad \Vert +3\\ y&=4x-5 \\ \end{align*}