Suorakulmaisen kolmion trigonometriaa

Kuva 1

Kuva 2

Trigonometriassa tarkastellaan kulmien ja pituuksien suhteita. Palautetaan ensin mieleen aikaisemmin opeteltuja asioita:

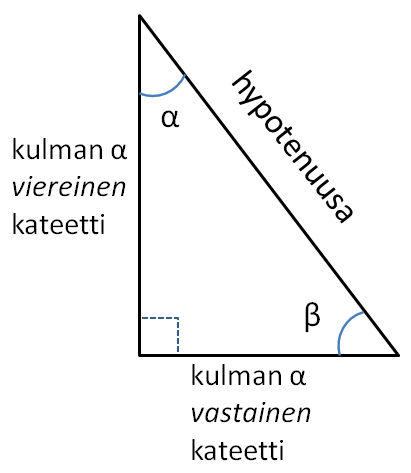
Suorakulmaisesta kolmiosta saadaan seuraavat määritelmät:

\begin{align*} \sin\alpha &= \frac{ \:\text{kulman}\: \alpha \:\text{vastaisen kateetin pituus}}{ \:\text{hypotenuusan pituus}} \\ \cos\alpha &= \frac{ \:\text{kulman}\: \alpha \:\text{viereisen kateetin pituus}}{ \:\text{hypotenuusan pituus}} \\ \tan\alpha &= \frac{ \:\text{kulman}\: \alpha \:\text{vastaisen kateetin pituus}}{ \:\text{kulman}\: \alpha \:\text{viereisen kateetin pituus}} \end{align*}

Yllä sana pituus jätetään toisinaan pois, mutta kysymys on aina sivujen pituuksista.

Esimerkkitehtävä

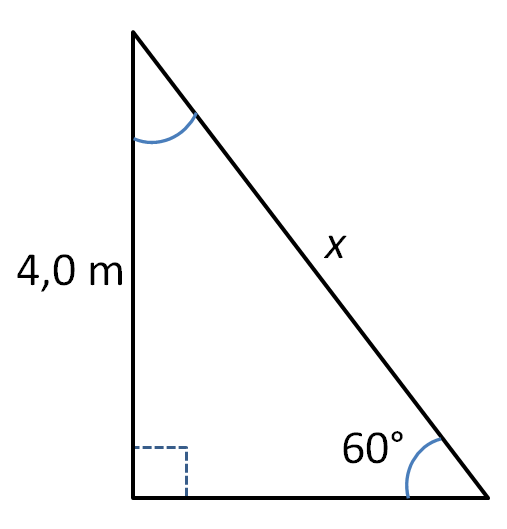
Laske kuvan 2 kolmion hypotenuusan pituus.

Ratkaisu: kolmiosta tunnetaan kulma ja sen vastainen kateetti, ja hypotenuusan pituus pitäisi selvittää. Käytetään siis sinifunktiota. Yksikkö voidaan jättää pois yhtälöstä kunhan pidetään mielessä, että metreistä puhutaan:

\begin{align*} \sin60°&=\frac{4,0}{x}\quad \Vert \cdot x \\ x \cdot \sin60°&=4,0 \quad \Vert :\sin60° \\ x&=\frac{4,0}{\sin60°}≈4,6 \\ \end{align*}

Vastaus: hypotenuusa on noin \(4,6\) metriä pitkä.