Toisen asteen yhtälö

Kuva 1

Kuva 2

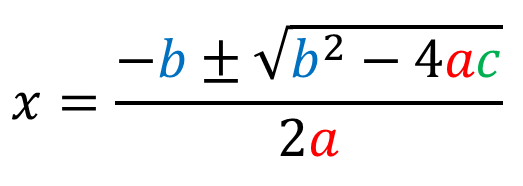Yhtälö on toista astetta, jos sen puolet ovat polynomeja, joista korkeamman (tai molempien) aste on 2.

Muistutus: polynomin aste on muuttujan suurin eksponentti.

Esimerkiksi yhtälö \(x^{2}-3x=6\) on toisen asteen yhtälö.

Yleinen muoto: \(ax^{2}+bx+c=0\), missä \(a\), \(b\) ja \(c\) ovat reaalilukuja.

Vaillinainen muoto: \(ax^{2}+c=0\) tai \(ax^{2}+bx=0\), missä \(a\), \(b\) ja \(c\) ovat reaalilukuja

Ratkaisumenetelmiä

• Ratkaisukaava toimii aina (yhtälö ensin nollamuotoon): \(\displaystyle{x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}}\)
• Tulon nollasääntö (tekijöihin jako ei aina helppoa): näppärä muodon \(ax^{2}+bx=0\) vaillinaisissa yhtälöissä sekä niissä tapauksissa, joissa muistikaavat toimivat.
• Vaillinainen muoto \(ax^{2}+c=0\): ensin \(x^{2}\) yksin yhtälön toiselle puolelle ja sitten otetaan neliöjuuri yhtälön kummastakin puolesta. Muista \(\pm\)!

Esimerkki:

Yhtälössä \(x^{2}+x-6=0\) vakiota \(a\) vastaa luku \(1\), vakiota \(b\) luku \(1\) ja vakiota \(c\) luku \(-6\). Yhtälön ratkaisu saadaan ratkaisukaavaan sijoittamalla seuraavasti:

\begin{equation} x=\frac{-1\pm \sqrt{1^{2}-4 \cdot 1 \cdot \left (-6\right )}}{2 \cdot 1} =\frac{-1\pm \sqrt{1+24}}{2} =\frac{-1\pm 5}{2} \end{equation}

Tulokseksi saadaan, että tuntemattomalla on kaksi eri arvoa. Lasketaan ne erikseen:

\(x=\frac{-1+ 5}{2}=\frac{4}{2}=2\) tai \(x=\frac{-1- 5}{2}=\frac{-6}{2}=-3\)

Ratkaisu: \(x = 2\) tai \(x=-3\). Sijoittamalla arvot alkuperäiseen yhtälöön huomataan, että kummallakin arvolla yhtälön puolista tulee samat luvut (nolla). Ratkaisut ovat siis oikeita.