Määrittelyjoukko

Kuva 1

Kuva 1

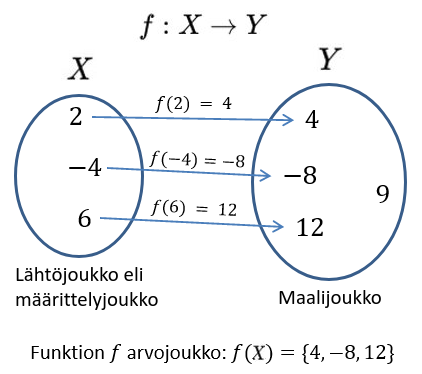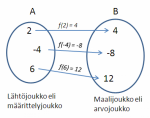
Funktion määrittelyjoukko on niiden lukujen joukko, joilla funktio antaa järkevän tuloksen.

Funktio merkitään usein merkinnällä (joukkoja merkitsevät kirjaimet vaihtelevat eri lähteissä)

\begin{equation*}f: X \to Y\end{equation*}

jossa joukko \(X\) on funktion määrittelyjoukko ja \(Y\) maalijoukko. Merkintä luetaan "funktio f joukosta X joukkoon Y". Tämä merkitsee sitä, että funktio yhdistää jokaisen joukon \(X\) arvon johonkin joukon \(Y\) arvoon.

Ellei muuta ole mainittu, määrittelyjoukkoon kuuluvat kaikki luvut, joilla funktion arvo on määritelty. Joissakin tapauksissa määrittelyjoukkoa rajoitetaan muusta syystä (esimerkiksi käytännön tilanteeseen liittyvät rajoitukset).

Koulumatematiikassa "kaikki luvut" viittaa yleensä reaalilukujen joukkoon \(\mathbb{R}\), ellei muuta mainita. Funktion \(f\) määrittelyjoukkoa voidaan merkitä symbolilla \(M_f\).

Esimerkki 1: Kaikki polynomifunktiot ovat määriteltyjä kaikilla reaaliluvuilla, joten funktion \(f(x)=x^2-5\) määrittelyjoukko on \(M_f=\mathbb{R}\).

Esimerkki 2: Funktio \(g(x)=\frac{1}{x+1}\) on määritelty kaikilla muilla paitsi luvulla \(-1\), koska tällöin pitäisi jakaa nollalla. Määrittelyjoukko "kaikki muut reaaliluvut paitsi \(-1\)" voidaan merkitä seuraavasti: \begin{equation*}M_g = \mathbb{R}\: \backslash \{-1\}. \end{equation*} Usein sama merkitään määrittelyehdon avulla lyhyesti \(x\neq -1\).

Esimerkki 3: Funktio \(h(x)=\ln{(x-3)}\) on määritelty kaikilla luvuilla, jotka ovat suurempia kuin luku \(3\). Määrittelyehto on täten \(x > 3\) ja määrittelyjoukko voidaan merkitä hakasulkujen avulla näin: \begin{equation*}M_h = ]3, \infty [ \end{equation*}

Määrittelyjoukkoa nimitetään joskus lähtöjoukoksi.