Arvojoukko

Kuva 1

Funktion arvojoukko on kaikkien funktion arvojen joukko. Muista, että funktion arvo on koordinaatistossa kuvaajan korkeus eli \(y\)-koordinaatti. Merkinnässä (huomaa, että isot kirjaimet viittaavat joukkoihin)

\begin{equation*} f: X \to Y \end{equation*}

maalijoukko \(Y\) sisältää funktion arvojoukon \(f(X)\), mutta maalijoukko voi sisältää muitakin arvoja. Arvojoukko on siis maalijoukon osajoukko eli \(f(X) \subset Y\).

Arvojoukolle käytetään joskus merkintää \(A_f\), jossa kirjain \(A\) tulee sanasta arvojoukko ja alaindeksi viittaa funktion nimeen (tässä \(f\)).

Esimerkki

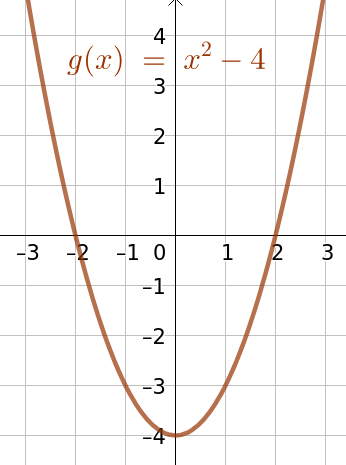
Funktion \(g(x)=x^{2}-4\) kuvaaja on ylöspäin aukeava paraabeli (Kuva 1). Toisen asteen termi on aina positiivinen, joten funktion pienin arvo on \(g(0)=0^{2}-4=-4\). Funktio saa myös kaikki tuota suuremmat arvot, joten funktion \(g\) arvojoukko on \([-4, \infty [\). Tämä voidaan merkitä lyhyesti \(A_g=[-4, \infty[\).