Logaritmifunktion määrittely- ja arvojoukko

Kuva 1

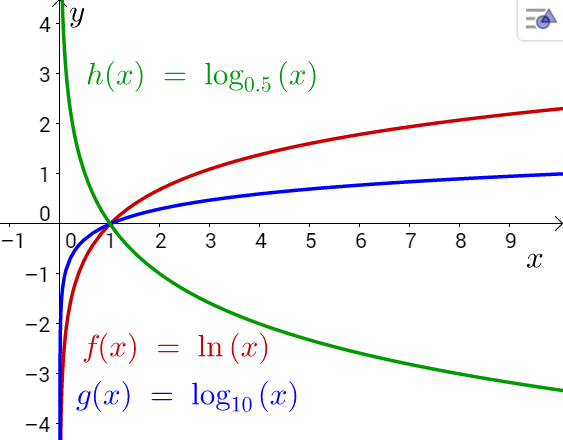Olkoon vakio \(a>0\), \(a\neq 1\) ja funktio \(f(x)=\log_a{x}\).

Määrittelyjoukko

Funktio \(f(x)\) on määritelty, kun \(x>0\), eli funktion määrittelyjoukko on \(\mathbb{R}_{+}\) (positiivisten reaalilukujen joukko).

Tämä johtuu siitä, että positiivisen luvun \(a\) potenssi on aina positiivinen, joten kaikilla luvuilla \(b\) pätee \(a^b > 0\).

Arvojoukko

Kun kantaluku \(a > 1\), funktion \(f(x)\) arvo, eli \(a\)-kantaisen eksponentin arvo lähestyy ääretöntä, kun \(x\to \infty \), ja negatiivista ääretöntä, kun \(x\to 0 \). Kun kantaluku \(0 < a < 1\), menevät ääriarvot toisin päin, eli \(\displaystyle{\lim_{x\to \infty}f(x)=-\infty}\) ja \(\displaystyle{\lim_{x\to 0}f(x)=\infty}\).

Logaritmifunktio on jatkuva määrittelyjoukkossaan, joten se saa kaikki arvot väliltä \(]-\infty, \infty[\). Funktion arvojoukko on siis koko reaalilukujen joukko \(\mathbb{R}\).

Merkintä

Yllä olevat seikat voidaan merkitä ytimekkäästi seuraavalla merkinnällä: \begin{equation*}f: \mathbb{R}_+\to \mathbb{R}\end{equation*}