Pinta-alalaskut (osa 1)

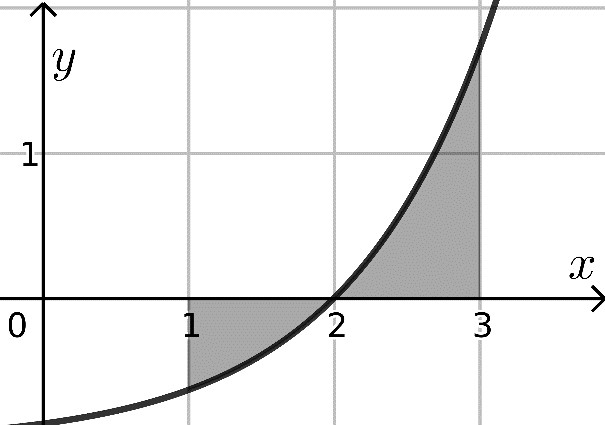
Kuva 1

Pinta-ala lasketaan määrätyn integraalin avulla. Laskin saattaa osata laskea suoraan itseisarvokaavasta, mutta käsin laskiessa pitää päästä eroon itseisarvomerkeistä ensin.

Kahden kuvaajan väliin jäävä pinta-ala:

\begin{equation} A=\int\limits_{a}^{b}\left |f(x)-g(x)\right | \mathrm{d}x \label{alaint1} \end{equation}

Kaavalla \(\eqref{alaint1}\) lasketaan kahden funktion \(f\) ja \(g\) väliin jäävä pinta-ala välillä \([a,b]\).

Kuvaajan ja \(x\)-akselin välinen ala:

Kun toinen funktioista on nollafunktio (x-akseli), saadaan pinta-ala integroimalla toinen funktio (alla \(f(x)\)):

\begin{equation} A=\int\limits_{a}^{b}\left|f(x)\right | \mathrm{d}x \label{alaint2} \end{equation}

Käsin laskiessa täytyy poistaa itseisarvomerkit. Sitä varten tarkistetaan, ylittääkö funktion kuvaaja \(x\)-akselia välillä \([a,b]\). Jos näin on, pitää integraali laskea useammassa osassa, jotta etumerkit menevät oikein.

Esimerkki

Kuvassa 1 on funktion \(f(x)\) kuvaaja ja tarkoitus on laskea varjostettujen alueiden pinta-ala. Kuvaaja ylittää x-akselin kohdassa \(x=2\), joten pinta-ala pitää laskea kahdessa osassa:

\begin{equation*} A=\int\limits_{1}^{3}\left|f(x)\right | \mathrm{d}x =\int\limits_{1}^{2}-f(x) \mathrm{d}x+\int\limits_{2}^{3}f(x) \mathrm{d}x\\ =-\int\limits_{1}^{2}f(x) \mathrm{d}x+\int\limits_{2}^{3}f(x) \mathrm{d}x \end{equation*}

Käytännössä riittää muistaa, että jos kuvaaja kulkee x-akselin alapuolella, lisätään integraalin eteen miinusmerkki.