Suoran ja koordinaattiakseleiden leikkauspisteet

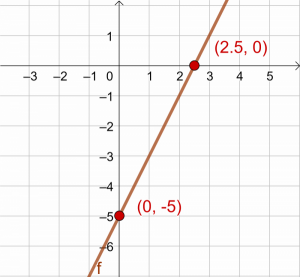
Kuva 1

Suora leikkaa yleensä sekä \(x\)- että \(y\)-akselin jossakin pisteessä. Poikkeuksia ovat suorat, jotka ovat pysty- tai vaakasuorassa. Tällaiset suorat leikkaavat vain toisen koordinaattiakseleista.

1) Suoran ja y-akselin leikkauspisteen määrittäminen:

Piste on aina y-akselilla, kun pisteen x-koordinaatti on nolla. Kun sijoitetaan \(x=0\) suoran yhtälöön, saadaan seuraava tulos:

\begin{equation*} y=kx+b = k \cdot 0 +b = b\end{equation*}

Termi \(kx\) häviää ja jäljelle jää vain vakio \(b\). Näin ollen suoran ja \(x\)-akselin leikkauspiste on aina \((0, b)\), kun suora ei ole pystysuorassa.

2) Suoran ja \(x\)-akselin leikkauspisteen määrittäminen:

Piste on aina \(x\)-akselilla, kun pisteen \(y\)-koordinaatti on nolla. Kun suoran yhtälön oikea puoli (\(=y\)) yhtä suureksi kuin \(0\), saadaan muuttujan \(x\) arvo ratkaisemalla yhtälö.

Esimerkki (kuva 1): olkoon suora \(y=2x-5\). Suoran ja \(y\)-akselin leikkauspisteen \(x\)-koordinaatti on nolla ja \(y\)-koordinaatti yhtälön vakiotermi \(-5\), joten suora leikkaa \(y\)-akselin pisteessä (\(0,-5\)).

Suoran ja \(x\)-akselin leikkauspisteessa korkeus eli \(y\) on nolla. Muodostetaan yhtälö ja ratkaistaan se:

\begin{align*} y&=2x-5 \quad \Vert\: \:\text{sij. }y=0\\ 0&=2x-5 \quad \Vert+5 \\ 5&=2x \quad \Vert:2\\ \frac{5}{2} &=x \\ x &=\frac{5}{2}=2\frac{1}{2} \end{align*}

Suora leikkaa siis x-akselin pisteessä (\(2\frac{1}{2},0\)).