Funktion nollakohta

Kuva 1

Funktion \(f(x)\) nollakohtia ovat kaikki ne muuttujan \(x\) arvot, joilla funktion arvo \(f(x)=0\).

Funktion kuvaaja leikkaa nollakohdassa \(x\)-akselin tai ainakin käy \(x\)-akselilla. Tällöin funktion arvo eli \(y\) on nolla.

Nollakohtia funktiolla ei välttämättä ole. Toisaalta nollakohtia voi olla rajattoman paljon, jos funktion kuvaaja ylittää \(x\)-akselin toistuvasti.

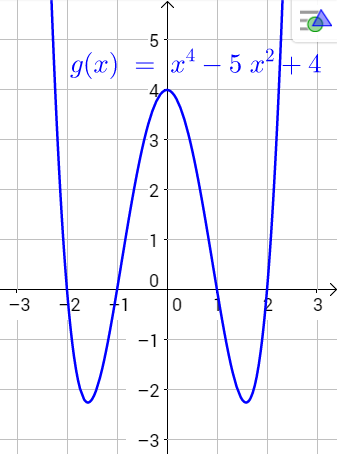
Kuvassa 1 on funktion \(g(x)=x^{4}-5x^{2}+4\) kuvaaja, joka ylittää \(x\)-akselin neljässä kohdassa. Funktion nollakohdat ovat kuvasta arvioiden \(x=-2\), \(x=-1\), \(x=1\) ja \(x=2\).

Esimerkki: funktion \(f(x)=x^{2}-4\) nollakohdat saadaan selville ratkaisemalla yhtälö \(x^{2}-4=0\).

$$\begin{align*} x^{2}-4&=0 \\ x^{2}&=4 \quad \Vert\sqrt{} \\ \left |x\right |&= \sqrt{4} = 2 \\ x=& \pm 2\end{align*}$$

Funktion \(f(x)=x^{2}-4\) nollakohdat ovat \(x=\pm2\).