Nollakohtien laskeminen (1. ast. funk.)

Kuva 1

Funktion nollakohdat lasketaan merkitsemällä funktion arvo nollaksi ja ratkaisemalla syntyvä yhtälö.

Funktion \(f(x)\) nollakohdat ovat ne muuttujan \(x\) arvot, jotka toteuttavat yhtälön \(f(x)=0\).

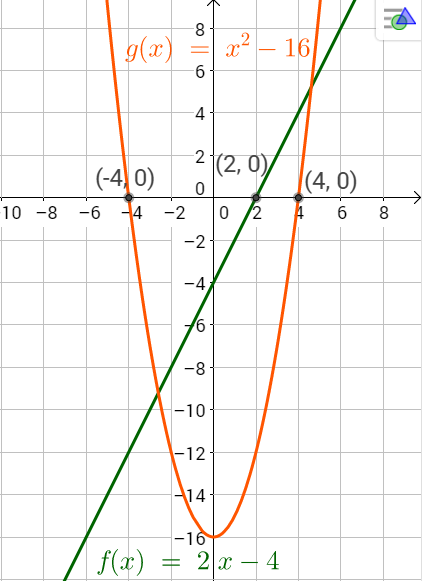
Esimerkki 1: funktion \(f(x)=2x-4\) nollakohta saadaan selville ratkaisemalla yhtälö \(2x-4=0\).

$$\begin{align*} 2x-4&=0 \quad \Vert+4\\ 2x&=4 \quad \Vert:2 \\ x&=2 \end{align*}$$

Funktion \(f\) nollakohta on \(x=2\). Tällöin funktion kuvaaja (suora) ylittää \(x\)-akselin pisteessä \((2,0)\). Kuvassa 1 on piirretty kyseinen suora.