\(\sin^2x+\cos^2x = 1\)

Kuva 1

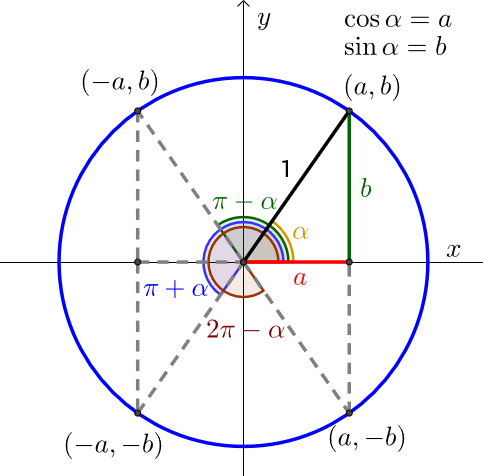Huomaa, että kuvassa kulma on merkitty kreikkalaisen aakkosen \(\alpha\) avulla, jottei se mene sekaisin koordinaatiston \(x\)-akselin kanssa. Sinänsä muuttujakirjaimella ei ole merkitystä (kreikkalaisella aakkosella saatetaan viitata asteina annettuun kulmaan ja latinalaisella aakkosella radiaaneina annettuun, mutta sama kulma se on kuitenkin).

Kuvan yksikköympyrästä nähdään, että kulman \(\alpha \) sini on merkityn kehäpisteen y-koordinaatti (kolmion korkeus) ja vastaavasti kulman \(\alpha \) kosini kehäpisteen x-koordinaatti (kolmion leveys).

Koska yksikköympyrän säde on 1, antaa suorakulmaisen kolmion sivujen pituuksiin liittyvä Pythagoraan lause \(a^2+b^2=c^2\) suoraan väitetyn yhtäsuuruuden:

\((\sin \alpha )^2+(\cos \alpha)^2 = 1\)

eli

\(\sin^2 \alpha+\cos^2 \alpha = 1\)

tai kirjainten \(x\) ja \(y\) avulla:

\(\sin^2x+\cos^2x = 1\)

Huomaa, että yhtäsuuruus toimii myös negatiivisilla kehäpisteen koordinaattien arvoilla, koska toiseen korottaminen neutralisoi miinuksen. Näitä tapauksia kuvassa esittävät katkoviivoilla piirretyt suorakulmaiset kolmiot. Lause on siis voimassa kaikilla mahdollisilla kulman arvoilla.