Potenssifunktioon perustuva mallinnus

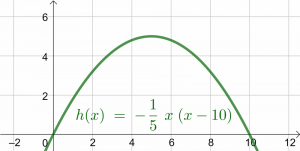
Kuva 1: vuoren sivuprofiili

Kahden muuttujan välistä suhdetta kuvataan toisinaan potensseja sisältävän lausekkeen avulla

Esimerkiksi vapaasti putoavan kappaleen kulkema matka on suoraan verrannollinen kuluneen ajan toiseen potenssiin (ellei ilmanvastusta oteta huomioon).

Tällaisissa tapauksissa laskut johtavat yleensä yhtälöihin, joiden puolet ovat eriasteisia polynomeja. Usein pärjätään toisen asteen yhtälöillä, mutta toisinaan törmätään hankalampiinkin tapauksiin.

Esimerkki

Erään vuoren sivuprofiili seuraa varsin tarkasti funktion \(h(x)=-\frac{1}{5}x^2+2x\) kuvaajaa. Toisin sanoen funktio antaa vuoren korkeuden kilometreinä, kun nollataso (\(x\)-akseli) kuvaa normaalia maanpinnan tasoa. Muuttujan \(x\) yksikkö on myös kilometri. Ylhäältä katsottuna vuori on ympyrän muotoinen.

Kysymykset:

1. Vuoren juuren lävistää keskeltä vaakasuora tunneli. Kuinka pitkä se on?
2. Kuinka pitkälle tunnelia pitää kulkea, kunnes ollaan vuoren huipun kohdalla?
3. Kuinka korkea vuori on?

Vastaukset

1. Funktion nollakohtien erotus antaa vuoren vaakasuoran läpimitan. Merkitään funktio nollaksi \(h(x)=0\) ja ratkaistaan syntyvä yhtälö \(-\frac{1}{5}x^2+2x=0\). Saadaan kaksi ratkaisua, nolla ja 10. Tämä merkitsee, että vuoren läpimitta, eli myös tunnelin pituus on 10 km. Vastaus: 10 km.
2. Kuvaaja on suora paraabeli, jonka huippu on täsmälleen nollakohtien puolessavälissä. Vastaus: Tunnelia pitää kulkea viisi kilometriä.
3. \(h(5)=-\frac{1}{5} \cdot 5^2+2 \cdot 5 = -5+10 =5\). Vastaus: vuori on viiden kilometrin korkuinen.