Binomin potenssit \((x+1)^n\) ja Pascalin kolmio

Pascalin kolmio

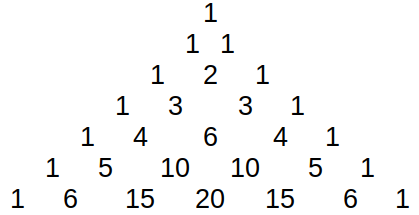Tarkastellaan muotoa \((x+1)^n\) olevia funktioita, kun \(n \in\mathbb{N}\). Laskin auttaa pitemmälle menevien potenssien sieventämisessä:

• \((x+1)^0=1\)
• \((x+1)^1=x+1\)
• \((x+1)^2=x^2+2x+1\)
• \((x+1)^3=x^3+3x^2+3x+1\)
• \((x+1)^4=x^4+4x^3+6x^2+4x+1\)
• \((x+1)^5=x^5+5x^4+10x^3+10x^2+5x+1\)
• \((x+1)^6=x^6+6x^5+15x^4+20x^3+15x^2+6x+1\)

Termien kertoimet näyttävät noudattavan symmetristä kaavaa. Tämä tulee näkyviin, jos asetetaan kertoimet kolmion muotoiseen asetelmaan, kuten kuvassa 1. Tällaista asetelmaa nimitetään Pascalin kolmioksi. Sen luvut saadaan helposti niin, että reunoille tulee aina ykköset ja muuten lasketaan yhteen kaksi yläpuolella olevaa vierekkäistä lukua.

Huomaa, ettei binomin toisen termin tarvitse olla \(1\). Esimerkiksi binomin \(a+b\) potenssien kertoimet noudattavat samaa kaavaa.