Leipurit ja Venn-diagrammi

Ehdollisessa todennäköisyydessä tapahtuman 1 todennäköisyyteen vaikuttaa jokin tapahtunut tai oletettu toinen tapahtuma 2. Tämä muuttaa tapahtuman 1 otosavaruutta, jolloin myös sen todennäköisyys usein muuttuu.

Venn-diagrammin avulla voidaan havainnollistaa otosavaruuden (perusjoukon) muuttumista. Tarkastellaan tunnettua leipuriesimerkkiä. Kullekin piparille saadaan seuraavat mahdolliset todennäköisyydet:

\begin{align*} &P(A\cap \text{rikki}) = P(A)\cdot P(\text{rikki}\vert A) = \frac{3}{4}\cdot \frac{1}{9} = \frac{1}{12} \\ &P(A\cap \text{ok}) = P(A)\cdot P(\text{ok}\vert A) = \frac{3}{4}\cdot \frac{8}{9} = \frac{2}{3} \\ &P(B\cap \text{rikki}) = P(B)\cdot P(\text{rikki}\vert B) = \frac{1}{4}\cdot \frac{1}{4} = \frac{1}{16} \\ &P(B\cap \text{ok}) = P(B)\cdot P(\text{ok}\vert B) = \frac{1}{4}\cdot \frac{3}{4} = \frac{3}{16} \\ \end{align*}

Kysytty todennäköisyys oli \(P(A\vert\text{rikki})\). Piirretään ensin Venn-diagrammi yllä mainituista todennäköisyyksistä:

Kuva 1

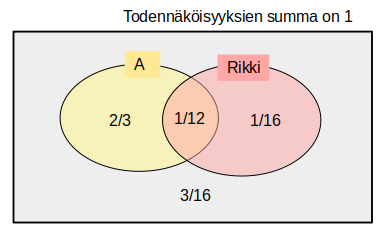Todennäköisyydessä \(P(A\vert\text{rikki})\) rajoitutaan tarkastelemaan pelkästään rikkinäisiä pipareita. Venn-diagrammissa soikio "Rikki" näyttää kyseisen otosavaruuden, jonka suotuisan tapahtuman todennäköisyys on 1/12 (leipurin A leipoma ja rikkoma pipari). Kysytty todennäköisyys saadaan nyt jakamalla tämä rikkinäisten todennäköisyyksien summalla (pinkki soikio):

\begin{equation*}P(A\vert\text{rikki}) = \frac{\frac{1}{12}}{\frac{1}{12}+\frac{1}{16}} = \frac{\frac{1}{12}}{\frac{4}{48}+\frac{3}{48}}=\frac{\frac{1}{12}}{\frac{7}{48}}=\frac{1}{12}\cdot\frac{48}{7}=\frac{4}{7}\end{equation*}

Vastaus: Pojan ottama pipari on kokeneemman leipurin tekemä todennäköisyydellä \(\frac{4}{7}\).