Leipurit ja puukaavio

Puukaavio on yksi parhaista työkaluista peräkkaisten tapahtuminen tapauksessa. Kaavio antaa helposti ymmärrettävän esityksen mahdollisista tapahtumaketjuista. Oheisessa puukaaviossa (kuva 1) on esitetty kaikki mahdolliset piparin kohtalot, joita on tässä neljä erilaista: kaksi leipuria ja kummallakin kaksi mahdollista lopputulosta (rikki tai ehjä).

Kuva 1

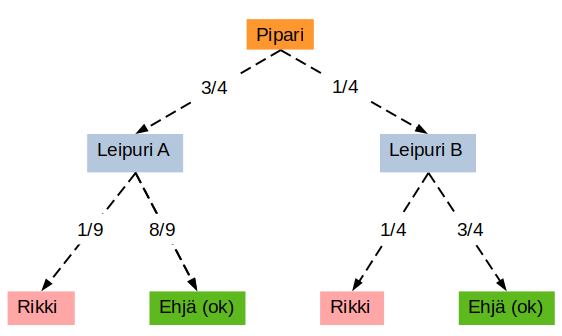Kysytty todennäköisyys \(P(A|\text{rikki})\) kertoo todennäköisyyden sille, että rikkinäisistä pipareista satunnaisesti valittu pipari on leipurin A koristelema. Tämä saadaan selville jakamalla puun vasemmanpuoleisimman oksan todennäköisyys rikkinäisen piparin todennäköisyydellä (kaksi oksaa eli yksittäisten oksien summa):

\begin{align*} P(A\vert\text{rikki}) &= \frac{\frac{3}{4} \cdot \frac{1}{9}}{\frac{3}{4} \cdot \frac{1}{9}+\frac{1}{4} \cdot \frac{1}{4}} =\frac{\frac{1}{12}}{\frac{1}{12}+\frac{1}{16}} \\ &= \frac{\frac{1}{12}}{\frac{4}{48}+\frac{3}{48}} =\frac{\frac{1}{12}}{\frac{7}{48}} =\frac{1}{12}\cdot\frac{48}{7} =\frac{4}{7} \end{align*}

Vastaus: Pojan ottama pipari on kokeneemman leipurin tekemä todennäköisyydellä \(\frac{4}{7}\).