Tehtävä 0: Kosinifunktiokysymyksiä (22.05.2019)

Kuva 1

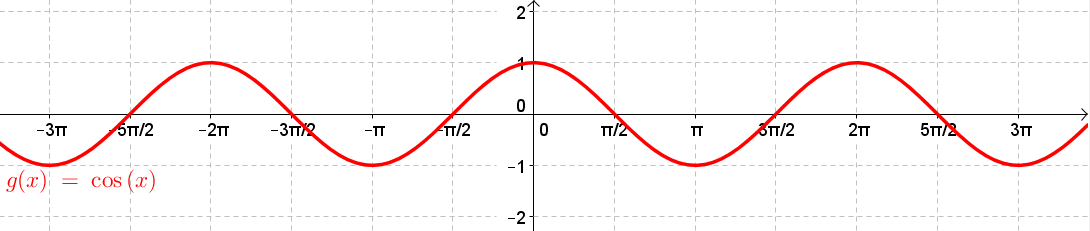Kuvassa 1 on kosinifunktion \(g(x)=\cos(x)\) kuvaaja. Päättele kuvaajan avulla vastaukset kysymyksiin. Vain viimeinen on tarkoitus tehdä laskimella.

1. Mikä on funktion jakson pituus eli matka kuvaajan ”aallonhuipulta” toiselle?
2. Millä muuttujan \(x\) arvoilla funktio on nolla?
3. Mikä on funktion suurin ja pienin arvo?
4. Mikä on funktion \(g(x)\) derivaatan arvo kohdassa \(x=0\)?
5. Kuinka monta nollakohtaa kosinin derivaatalla näyttää olevan?
6. Piirrä tangentti funktiolle kohtaan \(x=-π/2\) ja laske sen avulla mahdollisimman tarkasti arvo \(g'(-π/2 )\).
7. Laske laskimella \(g'(-π/2 )\).